如图所示,质量为为m、电量为q的带电粒子,
经电压为U加速,又经磁感应强度为B的匀强磁场后落到图中D点,求:
(1)带电粒子在A点垂直射入磁场区域时的速率v;
(2)A、D两点间的距离l。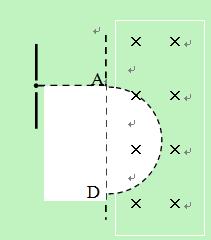
在某一星球上,从80m高处做自由落体的物体,在第1s内下落了4m,求:
(1)该物体3s末的速度;
(2)在6s内该物体下落的高度.
如图甲所示,有一足够长的粗糙斜面,倾角θ=37°,一滑块以初速度v0=16m/s从底端A点滑上斜面,滑至B点后又返回到A点。滑块运动的图象如图乙所示,(已知:sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2)。求:
(1)AB之间的距离;
(2)滑块再次回到A点时的速度;
如图所示, ,两物体与地面间的动摩擦因数均为0.2,当大小为F=5N水平拉力作用在物体A上时,求物体A的加速度。(忽略滑轮的质量以及滑轮和绳的,取
,两物体与地面间的动摩擦因数均为0.2,当大小为F=5N水平拉力作用在物体A上时,求物体A的加速度。(忽略滑轮的质量以及滑轮和绳的,取 )
)
一小汽车由静止开始匀加速启动,加速度a=2.5m/s2,其最大速度为Vm=3m/s,试求它在t=5s内发生的位移。
一静止的带电粒子电荷量为q、质量为m(不计重力),从P点经电场强度为E的匀强电场加速。运动了距离L之后经A点进入右边的有界磁场B1,穿过B1后再进入空间足够大的磁场B2,B1和B2的磁感应强度大小均为B,方向相反,如图所示。若带电粒子能按某一路径再由点A回电场并回到出发点P,而重复前述过程(虚线为相反方向的磁场分界面,并不表示有什么障碍物),求:
(1)粒子经过A点的速度大小;
(2)磁场B1的宽度d为多大;
(3)粒子在B1和B2两个磁场中的运动时间之比?