某班进行个人投篮比赛,有1人未进球,有2人各进一球,有7人各进2球,有2人各进5球,没有人进5球以上,小英和一些同学各进3球,小亮和一些同学各进4球.已知进球3个或3个以上的同学平均进3.5个球,进球4个或4个以下的同学平均每人进2.5个球,问进3个球和进4个球的人数各是多少?
PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据PM2.5检测网的空气质量新标准,从德州市2013年全年每天的PM2.5日均值标准值(单位:微克/立方米)监测数据中随机地抽取25天的数据作为样本,并根据检测数据制作了尚不完整的频数分布表和条形图:

(1)求出表中m,n,a的值,并将条形图补充完整;
(2)以这25天的PM2.5日均值来估计该年的空气质量情况,估计该年(365天)大约有多少天的空气质量达到优或良;
(3)请你结合图表评价一下我市的空气质量情况.
如图,已知矩形OABC的A点在x轴上,C点在y轴上,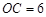 ,
,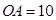 .
.
(1)在BC边上求作一点E,使OE=OA;(保留作图痕迹,不写画法)
(2)求出点E的坐标.
化简求值: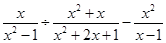 ,其中
,其中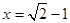 .
.
如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.有下列结论:
①∠DEO=45°;
②△AOD≌△COE;
③S四边形CDOE =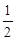 S△ABC;
S△ABC;
④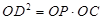 .
.
其中正确的结论序号为 .(把你认为正确的都写上)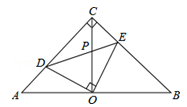
在图①至图③中,已知△ABC的面积为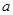 .
.
(1)如图①,延长△ABC的边BC到点D,使CD=BC,连结DA。若△ACD的面积为S1,则S1=______(用含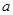 的代数式表示);
的代数式表示);
(2)如图②,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则S2=__________(用含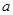 的代数式表示);
的代数式表示);
(3)在图①—②的基础上延长AB到点F,使BF=AB,连结FD,FE,得到△DEF(如图③).
阴影部分的面积为S3,则S3=__________(用含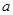 的代数式表示),并运用上述(2)的结论写出理由.
的代数式表示),并运用上述(2)的结论写出理由.
理由: