如图①,在矩形ABCD中,将矩形折叠,使B落在边AD(含端点)上,落点记为E,这时折痕与边BC或者边CD(含端点)交于F,然后展开铺平,则以B、E、F为顶点的三角形△BEF称为矩形ABCD的“折痕三角形”
(1)由“折痕三角形”的定义可知,矩形ABCD的任意一个“折痕△BEF”是一个 三角形
(2)如图②、在矩形ABCD中,AB=2,BC=4,,当它的“折痕△BEF”的顶点E位于AD的中点时,画出这个“折痕△BEF”,并求出点F的坐标;
(3)如图③,在矩形ABCD中,AB=2,BC=4,该矩形是否存在面积最大的“折痕△BEF”?若存在,说明理由,并求出此时点E的坐标?若不存在,为什么?
如图,在Rt△ABC中,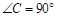 ,AB的垂直平分线与BC,AB的交点分别为D,E.
,AB的垂直平分线与BC,AB的交点分别为D,E.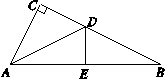
(1)若AD=10,
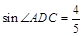 ,求AC的长和
,求AC的长和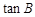 的值;
的值;(2)若AD=1,
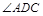 =
=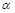 ,参考(1)的计算过程直接写
,参考(1)的计算过程直接写
出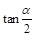 的值(用
的值(用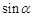 和
和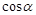 的值表示).
的值表示).
学校要围一个矩形花圃,花圃的一边利用足够长的墙,另三边用总长为36米的篱笆恰好围成(如图所示).设矩形的一边AB的长为x米(要求AB<AD),矩形ABCD 的面
积为S平方米.
(1)求S与
 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量 的取值范围;
的取值范围;(2)要想使花圃的面积最大,AB边的长应为多少米?
已知:如图,在菱形ABCD中,E为BC边上一点,∠AED=∠B.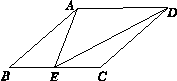
(1)求证:△ABE∽△DEA;
(2)若AB=4,求
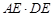 的值.
的值.
已知抛物线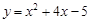 .
.(1)直接写出它与x轴、y轴的交点的坐标;
(2)用配方法将
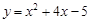 化成
化成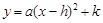 的形式.
的形式.
已知关于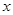 的方程
的方程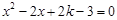 有两个不相等的实数根.
有两个不相等的实数根.(1)求
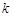 的取值范围;
的取值范围;(2)若
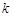 为符合条件的最大整数,求此时方程的根.
为符合条件的最大整数,求此时方程的根.