(本小题满分8分)
某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性
笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,
水性笔若干支(不少于4支).
(1)分别写出两种优惠方法购买费用y(元)与所买水性笔支数x(支)之间的函数关系式;
(2)对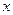 的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
(3)小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济.
解下列一元二次方程.
(1)x2-5x+1=0;
(2)3(x-2)2=x(x-2).
在平面直角坐标系中,已知抛物线 (a,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(﹣4,3),直角顶点B在第二象限.
(a,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(﹣4,3),直角顶点B在第二象限.
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;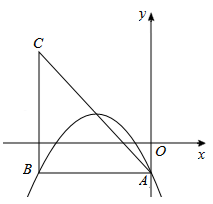
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q,判断线段PQ的长度是否为定值?如果是,求出PQ的长;如果不是,说明理由;
(3)在(2)的条件下,若点M在直线AC下方,且为平移前(1)中的抛物线上的点,以M、P、Q三点为顶点的三角形是等腰直角三角形,求出所有符合条件的点M的坐标.
如图,把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm,DC=7cm,把三角板DCE绕点C顺时针旋转15°得到△D′CE′,如图乙.这时AB与CD′相交于点O,D′E′与AB相交于点F,连接AD′.
(1)求∠OFE′的度数;
(2)求线段AD′的长;
(3)若把三角形D′C E′ 绕着点C顺时针再旋转30°得△D2CE2,这时点B在△D2CE2 的内部、外部、还是边上?证明你的判断.
以O为圆心的两个同心圆中,AD是大圆的直径,大圆的弦AB与小圆相切于点C,过C点作FH⊥AD交大圆于F、H,垂足为E.
(1)判断AC与BC的大小关系,并说明理由.
(2)如果FC、CH的长是方程x2-2 x+4=0的两根(CH>CF),求CE、CA的长以及图中阴影部分的面积.
x+4=0的两根(CH>CF),求CE、CA的长以及图中阴影部分的面积.
为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=-2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?