（本小题满分10分）如图1，点C将线段AB分成两部分，
如果AB : AC="AC" : BC，那么称点C为线段
的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线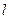
将一个面积为S的图形分成两部分，这两部分的面积分别为S1: S2，如果S : S1= S1: S2，，那么称直线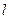为该图形的黄金分割线．
（1）研究小组猜想：在△ABC
中，若点D为AB边上的黄金分割点（如图2），则直线CD是△ABC的黄金分割线．你认为对吗？为什么？
（2）请你说明：三角形的中线是否也是该三角形的黄金分割线？
（3）研究小组探究发现：在（1）中，过点C任作AE交AB于E，再过点D作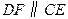
，交 AC于点F，连接EF（如图3），则直线EF是△ABC的黄金分割线．请说明理由．
（4）如图4，点E是
ABCD的边AB的黄金分割点，过点E作
，交DC于点F，显然直线EF是ABCD的黄金分割线．请你再画一条
ABCD的黄金分割线，使它不经过ABCD各边黄金分割点（保留必要的辅助线）．
我市某中学举行“中国梦•校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩如图所示．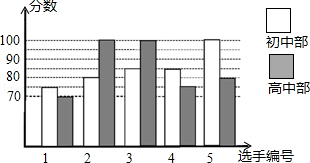
（1）根据图示填写下表；
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．
| 平均数 |
中位数 |
众数 |
|
| 初中部 |
|
85 |
|
| 高中部 |
85 |
|
100 |
如图，△ABC与△ADE关于直线MN对称．BC与DE的交点F在直线MN上．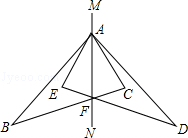
①指出两个三角形中的对称点；
②指出图中相等的线段和角；
③图中还有对称的三角形吗？
如图所示，
（1）在图a中把正方形分成四个全等的三角形；
（2）在图b中把正五边形分成五个全等的三角形；
（3）在图c中把正六边形分成六个全等的三角形？
（4）通过（1）（2）（3）的解答，你发现了什么规律？
如图，已知四边形ABCD和直线l，试在图形中作四边形A′B′C′D′，使四边形A′B′C′D′和四边形ABCD关于直线l对称．（不要求写作法，只仅留作图痕迹）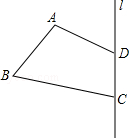
（本小题满分11分）在我市某一城市美化工程招标时，有甲、乙两个工程队投标，经测算：甲队单独完成这项工程需要60天，
若由甲队先做20天，剩下的工程由甲、乙合作24天可完成．
（1）乙队单独完成这项工程需要多少天？
（2）甲队施工一天，需付工程款3．5万元，乙队施工一天需付工程款2万元．若该工程计划在70天内完成，在不超过计划天数的前提下，是由甲队或乙队单独完成工程省钱？还是由甲乙两队全程合作完成该工程省钱？