(本小题满分14分)如图,在等腰梯形ABCD中,AB=DC=5,AD=4,BC="10." 点
E在下底边BC上,点F在腰AB上. 
(1)若EF平分等腰梯形ABCD的周长,设BE长为x,试用含x的代数式表示△BEF的面积;
(2)是否存在线段EF将等腰梯形ABCD的周长和面积同时平分?若存在,求出此时BE的长;若不存在,请说明理由;
(3)是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1∶2的两部分?若存在,求出此时BE的长;若不存在,请说明理由.
(本题14分)【问题探究】
(1)如图1,锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,四边形ABCD中,AB=3cm,BC=1cm,∠ABC=∠ACD=∠ADC=45°,求BD的长(结果保留根号).
(3)如图3,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长(结果保留根号).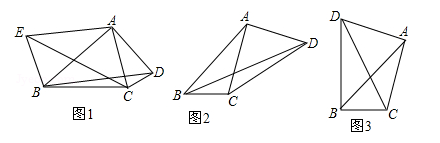
(本题12分)如图,有一个三角形ABC,三边为AC=6cm,BC=8cm,AB=10cm,沿AD折叠,使点C落在AB上的点E处,求线段CD的长.
(本题12分)已知:如图,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点,求证:MN⊥BD.
(本题10分)如图,我校实验大楼边上有一块空地需要绿化(即阴影部分),通过测量可以知道CD=6m,AD=8m,BC=24m,AB=26m,AD⊥CD,试求出这块空地的面积(即阴影部分面积).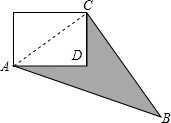
(本题8分)如图,△ABC中,AB=AC=CD,BD=AD,求△ABC中各角的度数.