(10分)如 图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3,
图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3,
连接BD,过点E作EM∥BD,交BA的延长 线于点M.
线于点M.

(1)求⊙O的半径;
(2)求证:EM是⊙O的切线;
(3)若弦DF与直径AB相交于点P,当∠APD=45º时,求图中阴影部分的面积.
已知反比例函数y=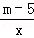 (m为常数,且m≠5).
(m为常数,且m≠5).
(1)若在其图象的每个分支上,y随x的增大而增大,求m的取值范围;
(2)若其图象与一次函数y=﹣x+1图象的一个交点的纵坐标是3,求m的值.
如图,一次函数y=kx+b与反比例函数y=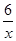 (x>0)的图像交于A(m,6),B(3,n)两点.
(x>0)的图像交于A(m,6),B(3,n)两点.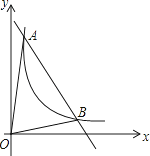
(1)求一次函数的解析式;
(2)根据图像直接写出使kx+b<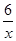 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积.
“低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班.王叔叔某天骑自行车上班从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
(1)①当t=2分钟时,速度v= 米/分钟,路程s= 米;
②当t=15分钟时,速度v= 米/分钟,路程s= 米.
(2)当0≤t≤3和3<t≤15时,分别求出路程s(米)关于时间t(分钟)的函数解析式;
(3)求王叔叔该天上班从家出发行进了750米时所用的时间t.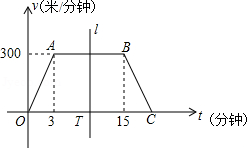
一次函数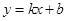 与反比例函数
与反比例函数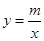 的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.
的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.
(1)求一次函数与反比例函数的表达式;
(2)过点B作BC⊥y轴,垂足为C,连接AC交x轴于点E,求△AED的面积S.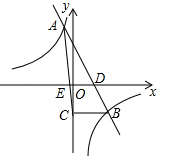
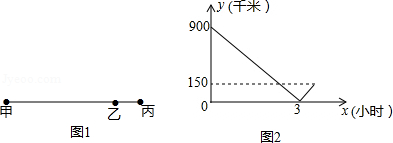
如图1所示,某乘客乘高速列车从甲地经过乙地到丙地,列车匀速行驶,图2为列车离乙地路程y(千米)与行驶时间x(小时)时间的函数关系图象.
(1)填空:甲、丙两地距离 千米.
(2)求高速列车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围.