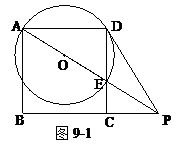
如图9-1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长 线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE = x,PC = y.
线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE = x,PC = y.
(1)求y与x之间的函数关系式;
(2)若PD是⊙O的切线,求x的值.
(3)过点D作DF⊥AE,垂足为H,交⊙O于点F,直线AF交BC于点G(如图9-2).若x=2,则sin∠BAG的值是_________.
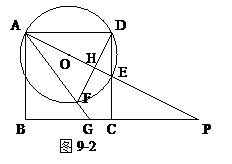
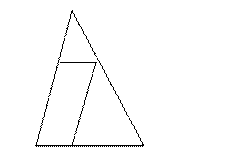
已知△ABC ,D、E、F分别是AB、AC、BC上的点。且DE∥BC, EF∥AB.
求证:
已知如图,AB和DE是直立在地面上的两根立柱,AB=10m,某一时刻AB在太阳光下的投影BC=6m.21世纪教育网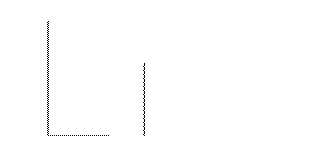
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为3m,计算DE的长.
某校九年级数学兴趣小组的同学开展了测量湘江宽度的活动.如图,他们在河东岸边的 点测得河西岸边的标志物
点测得河西岸边的标志物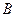 在它的正西方向,然后从
在它的正西方向,然后从 点出发沿河岸向正北方向行进550米到点
点出发沿河岸向正北方向行进550米到点 处,测得
处,测得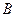 在点
在点 的南偏西60°方向上,他们测得的湘江宽度是多少米?(结果保留整数,参考数据:
的南偏西60°方向上,他们测得的湘江宽度是多少米?(结果保留整数,参考数据: ,
,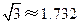 )
)
抛物线的顶点坐标为(2,-3),且过点(-1,7),求这条抛物线的解析式
在Rt△ABC中,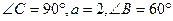 ,求
,求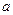 、
、 与
与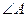 .
.