如图,正方形OABC的面积为9,点O为坐标原点,点B在函数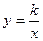
(k>0,x>0)的图象上,点P(m、n)是函数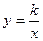 (k>0,x>0)的图象上任意一点,
(k>0,x>0)的图象上任意一点,
过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S.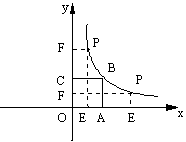
(1)求B点坐标和k的值;
(2)当S=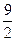 时,求点P的坐标。
时,求点P的坐标。
为迎接2020年第35届全国青少年科技创新大赛,某学校举办了 :机器人; :航模; :科幻绘画; :信息学; :科技小制作等五项比赛活动(每人限报一项),将各项比赛的参加人数绘制成如图两幅不完整的统计图.

根据统计图中的信息解答下列问题:
(1)本次参加比赛的学生人数是 名;
(2)把条形统计图补充完整;
(3)求扇形统计图中表示机器人的扇形圆心角 的度数;
(4)在 组最优秀的3名同学 名男生2名女生)和 组最优秀的3名同学 名男生1名女生)中,各选1名同学参加上一级比赛,利用树状图或表格,求所选两名同学中恰好是1名男生1名女生的概率.
如图,已知一次函数 的图象与反比例函数 的图象交于点 ,点 .
(1)求反比例函数的表达式;
(2)若一次函数图象与 轴交于点 ,点 为点 关于原点 的对称点,求 的面积.

(1)化简: ;
(2)解不等式: .
如图,菱形 的边长为1, ,点 是边 上任意一点(端点除外),线段 的垂直平分线交 , 分别于点 , , , 的中点分别为 , .
(1)求证: ;
(2)求 的最小值;
(3)当点 在 上运动时, 的大小是否变化?为什么?

已知抛物线 .
(1)求这条抛物线的对称轴;
(2)若该抛物线的顶点在 轴上,求其解析式;
(3)设点 , 在抛物线上,若 ,求 的取值范围.