设二次函数 的图像过原点,
的图像过原点, ,
, 的导函数为
的导函数为 ,且
,且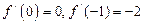 ,
,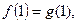

(1)求函数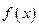 ,
,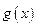 的解析式;(2)求
的解析式;(2)求 的极小值;
的极小值;
(3)是否存在实常数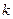 和
和 ,使得
,使得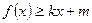 和
和 若存在,求出
若存在,求出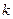 和
和 的值;若不存在,说明理由。
的值;若不存在,说明理由。
为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计。请你根据表中信息解答下列问题:
(1)若用系统抽样的方法抽取容量为50的一个样本,则写出表中的①②③④⑤填的数据;
(2)作出频率分布直方图;
(3)试估计参加这次竞赛的学生的平均成绩
(1)一本300页的书,随机打开一页,求页码在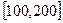 之间的概率。
之间的概率。
(2)在区间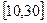 内的所有实数中,随机地取一个实数
内的所有实数中,随机地取一个实数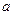 ,求实数
,求实数 的概率
的概率
已知 的3个顶点为
的3个顶点为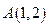 ,
, ,
, (1)求
(1)求 的值;
的值;
(2)求 的大小,并判断
的大小,并判断 的形状。
的形状。
(本小题16分)
首项为正数的数列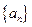 满足
满足


(I)证明:若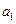 为奇数,则对一切
为奇数,则对一切 都是奇数;
都是奇数;
(II)若对一切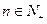 都有
都有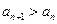 ,求
,求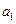 的取值范围.
的取值范围.
中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量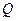 (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当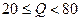 时,为酒后驾车;当
时,为酒后驾车;当 时,为醉酒驾车 淮安市公安局交通管理部门于2010年6月的一天对某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,
时,为醉酒驾车 淮安市公安局交通管理部门于2010年6月的一天对某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,
处醉酒驾车的有4人,依据上述材料回答下列问题:
(1)分别写出违法驾车发生的频率和醉酒驾车占违法驾车总数的百分数;
(2 )从违法驾车的10人中抽取4人,求抽取到醉酒驾车人数
)从违法驾车的10人中抽取4人,求抽取到醉酒驾车人数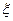 的分布列和期望;
的分布列和期望;
(3)饮酒后违法驾驶机动车极易发生交通事故,假设酒后驾车和醉酒驾车发生交通事故的概率分别是0.2和0.5,且每位驾驶员是否发生交通事故是相互独立的,依此计算被查处的10名驾驶员中至少有一人发生交通事故的概率