设奇函数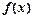 在(0,+∞)上为增函数,且
在(0,+∞)上为增函数,且 ,则不等式
,则不等式
的解集为( )
| A.(-1,0)∪(1,+∞) | B.(-∞,-1)∪(0,1) |
| C.(-∞,-1)∪(1,+∞) | D.(-1,0)∪(0,1) |
下表是某小卖部一周卖出热茶的杯数与当天气温的对比表:
| 气温/℃ |
18 |
13 |
10 |
4 |
-1 |
| 杯数 |
24 |
34 |
39 |
51 |
63 |
若热茶杯数y与气温x近似地满足线性关系,则其关系式最接近的是( )
A.y=x+6B.y=-x+42
C.y=-2x+60D.y=-3x+78
下表是某厂1~4月份用水量(单位:百吨)的一组数据:
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y |
4.5 |
4 |
3 |
2.5 |
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是=-0.7x+a,则a等于( )
| A.10.5 | B.5.15 | C.5.2 | D.5.25 |
从某大学随机选取8名女大学生,其身高x(cm)和体重y(kg)的回归方程为=0.849x-85.712,则身高172 cm的女大学生,由回归方程可以预报其体重( )
| A.为60.316 kg | B.约为60.316 kg |
| C.大于60.316 kg | D.小于60.316 kg |
已知变量x,y呈线性相关关系,且回归方程为=3-2x,则变量x,y是( )
| A.线性正相关关系 |
| B.线性负相关关系 |
| C.线性相关 |
| D.由回归方程无法判断其正负相关 |
下列两个变量之间的关系中,哪个是函数关系( )
| A.学生的性别与他的数学成绩 |
| B.人的工作环境与健康状况 |
| C.女儿的身高与父亲的身高 |
| D.正三角形的边长与面积 |