如图,在直角坐标平面内,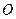 为原点,
为原点, 抛物线
抛物线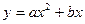 经过点
经过点 (
( ,
,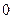 ),且顶点
),且顶点 (
( ,
,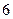 )在直线
)在直线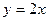 上.
上.
(1)求 的值和抛物线
的值和抛物线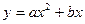 的解析式;
的解析式;
(2)如在线段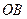 上有一点
上有一点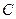 ,满足
,满足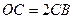 ,在
,在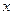 轴上有一点
轴上有一点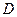 (
( ,
,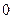 ),联结
),联结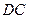 ,且直线
,且直线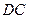 与
与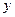 轴交于点
轴交于点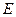 .
.
①求直线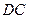 的解析式;
的解析式;
②如点M是直线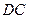 上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请求出点N的坐标.(直接写出结果,不需要过程.)
上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请求出点N的坐标.(直接写出结果,不需要过程.)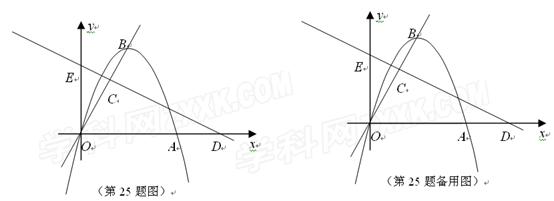
如图所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.
(1)画出四边形OABC关于y轴对称的四边形OA1B1C1,并写出点B1的坐标是;
(2)画出四边形OABC绕点O顺时针方向旋转90°后得到的四边形OA2B2C2;连结OB,求出OB旋转到OB2所扫过部分图形的面积.
如图,已知一架竹梯AB斜靠在墙角MON处,竹梯AB=13m,梯子底端离墙角的距离BO=5m.
(1)求这个梯子顶端A距地面有多高;
(2)如果梯子的顶端A下滑4 m到点C,那么梯子的底部B在水平方向上滑动的距离
BD="4" m吗?为什么?
(1)计算:
(2)已知: ,求
,求 的值.
的值.
如图,正方形ABCD的边长是2,M是AD的中点.点E从点A出发,沿AB运动到点B停止.连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连接EG、FG.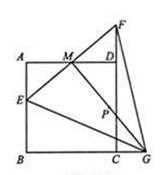
(1)设AE=x时,△EGF面积为y.求y关于x的函数关系式,并填写自变量x的取值范围;
(2)P是MG的中点,请直接写出点P运动路线的长.
某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单位应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元.设第二个月单价降低x元.
(1)填表(不需要化简)
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?