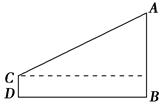
已知,边长为5的正方形ABCO在如图所示的直角坐标系中,点
M(t,0)为x轴上一动点,过A作直线MC的垂线交y轴于点N.
(1)当t=2时,求直线MC的解析式;
(2)设△AMN的面积为S,当S=3时,求t的值;
(3)取点P(1,y),如果存在以M、N、C、P为顶点的四边形是等腰梯形,当t<0时,甲同学说:y与t应同时满足方程t2-yt-5=0和y2-2t2-10y+26=0;乙同学说:y与t应同时满足方程t2-yt-5=0和y2+8t-24=0,你认为谁的说法 正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.
正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.
如图,一艘巡逻艇航行至海面B处时,得知正北方向上距B处20海里的C处有一渔船发生故障,就立即指挥港口A处的救援艇前往C处营救.已知C处位于A处的北偏东45°的方向上,港口A位于B的北偏西30°的方向上.求A、C之间的距离.(结果精确到0.1海里,参考数据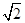 ≈1.41,
≈1.41,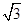 ≈1.73)
≈1.73)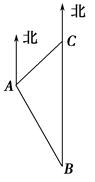
学校校园内有一小山坡AB,经测量,坡角∠ABC=30°,斜坡AB长为12米.为方便学生行走,决定开挖小山坡,使斜坡BD的坡比是1∶3(即为CD与BC的长度之比).A,D两点处于同一铅垂线上,求开挖后小山坡下降的高度AD.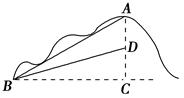
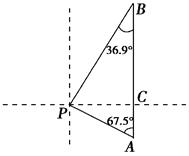
如图某天上午9时,向阳号轮船位于A处,观测到某港口城市P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到城市P位于该船的南偏西36.9°方向,求此时轮船所处位置B与城市P的距离?(参考数据:sin 36.9°≈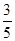 ,tan 36.9°≈
,tan 36.9°≈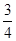 ,sin 67.5°≈
,sin 67.5°≈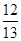 ,tan 67.5°≈
,tan 67.5°≈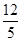 )
)
超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在A处,离益阳大道的距离(AC)为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为8秒,∠BAC=75°.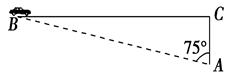
(1)求B、C两点的距离;
(2)请判断此车是否超过了益阳大道60千米/小时的限制速度?
(计算时距离精确到1米,参考数据:sin 75°≈0.965 9,cos 75°≈0.258 8,tan 75°≈3.732,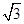 ≈1.732,60千米/小时≈16.7米/秒)
≈1.732,60千米/小时≈16.7米/秒)
如图,为了测量电线杆AB的高度,小明将测角仪放在与电线杆的水平距离为9 m的D处.若测角仪CD的高度为1.5 m,在C处测得电线杆顶端A的仰角为36°,则电线杆AB的高度约为________m(精确到0.1 m).(参考数据:sin 36°≈0.59,cos 36°≈0.81,tan 36°≈0.73)