如图所示,在水平向右的匀强电场中,长为L的绝缘细绳将一个质量为m的带电小球悬挂于O点,平衡时,小球位于B点,此时绳与竖直方向的夹角为θ(θ<45°)。已知重力加速度为g。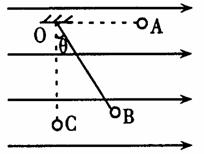
求:
(1)小球静止在B点时受到绳的拉力大小。
(2)若将小球拉到O点等高的A点(此时绳拉直),然后释放小球,当小球运动到最低点C时受到绳的拉力大小。
一跳伞运动员从静止在476m高空的直升机落下,开始未打开伞,自由下落一段高度后才打开伞以2 m/s2 的加速度匀减速下落,到达地面时的速度为4 m/s,试求运动员在空中自由下落的时间和在空中降落的总时间。(g=10m/s2)
一辆汽车以10m/s的初速度在水平地面上匀减速滑动,加速度大小为2m/s2,求:
(1)汽车在2s末的速度。
(2)汽车在6秒内的位移。
(3)汽车在最后1s内的平均速度。
如图所示,在空间中取直角坐标系Oxy,在第一象限内平行于y轴的虚线MN与y轴距离为d,从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场,场强大小为E。静止的电子经过另一个电势差为U的电场加速后,从y轴上的A点以平行于x轴的方向射入第一象限区域,A点坐标为(0,h)。已知电子的电量为e,质量为m,加速电场的电势差U> ,电子的重力忽略不计,求:
,电子的重力忽略不计,求:
(1)电子从A点进入电场到离开该电场区域所经历的时间t和离开电场区域时的速度v;
(2)电子经过x轴时离坐标原点O的距离l。
一个带正电的微粒,从A点射入水平方向的匀强电场中,微粒沿直线AB运动,如图,AB与电场线夹角θ=30°,已知带电微粒的质量m=1.0×10-7kg,电量q=1.0×10-10C,A、B相距L=20cm.(取g=10m/s2,结果保留二位有效数字)求: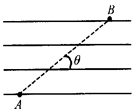
(1)说明微粒在电场中运动的性质,要求说明理由.
(2)电场强度的大小和方向?
(3)要使微粒从A点运动到B点,微粒射入电场时的最小速度是多少?
如图所示,已知电源电动势E=20V,内阻不计,当接入固定电阻R=4Ω时,电路中标有“3V, 6W”的灯泡L和内阻RD =0.5Ω的小型直流电动机D都恰能正常工作.试求: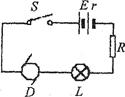
(1)电动机的额定电压;
(2)电动机的输出功率.