下表是甲地到乙地两条线路的有关数据：
| 线路 |
绕路 |
直路 |
| 路程 |
300公里 |
180公里 |
| 过路费 |
30元 |
90元 |
（1）若小车的平均速度为80公里/小时，则小车走直路比走弯路节省多少时间？
（2）若小车每公里的油耗为
升，按汽油价格为7.5元/升计算，
设走弯路的总费用为y1，走直路的总费用为y2，问x为何值时，所走哪条线路的总费用较少（总费用=过路费＋油耗费）；
（3）据道路管理部门统计：得到从甲地到乙地的五类不同油耗的小车平均每小时通过的车辆数，制成如图所示的频数分布直方图，请你估算每天早晨7点至晚上5点内这五类小车走直路比走弯路共节省多少升汽油．
小红家开了一家保暖内衣店，下表是去年一年12个月销售情况表：
根据上表回答问题：
（1）计算各季度的销量；
（2）用折线图表示（1）的销量情况；
统计图之间转换问题
2000年10万人中受教育程度的统计图如下;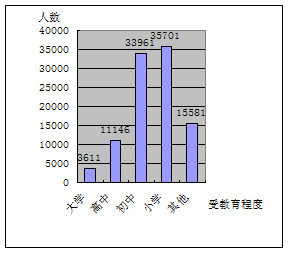
你能用扇形图描述数据吗？
某学校对二至九年级的学生做了关于视觉记忆和听觉记忆再现率的调查，结果如下;
听觉记忆：
视觉记忆：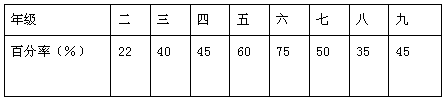
能否用扇形图表示所收集的数据？用何种统计图表示所收集的数据较合适？请画出。
到2000年，深圳市特区内、外总人口达到698万。其中福田区90万，南山区72万，盐田区15万，保安区273万，罗湖区77万，龙岗区171万
（1）根据以上数据制作统计表。
（2）用什么统计图可直观地描述各区的人口情况。
小明开了一家皮装专卖店，2005年各月份的销售情况如下表：
用合适的统计图表示2005年各季度的销售量变化情况。