如图，在△ACB中，∠ACB = 90°，AC = 4，BC = 2，点P为射线CA上的一个动点，以
为圆心，1为半径作
．
（1）连结
，若
，试判断与直线AB的位置关系，并说明理由；
（2）当PC为 时，与直线AB相切？当与直线AB相交时，写出PC的取值范围为 ；
（3）当与直线AB相交于点M、N时，是否存在△PMN为正三角形？若存在，求出PC的值；若不存在，说明理由．
分解因式：4x2y-4xy2+y3．
若5x-3y-2=0，则105x÷103y=。
如图，抛物线
与x轴交于A、B两点，与y轴交于点C（0，－3）．
（1）求k的值及点A、B的坐标；
（2）设抛物线的顶点为M，求四边形ABMC的面积；
（3）在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大?若存在，请求出点D的坐标；若不存在，请说明理由．
（4）在抛物线上求点Q，使△BCQ是以BC为直角边的直角三角形．
某商场将每件进价为160元的某种商品原来按每件200元出售，一天可售出100件，后来经过市场调查，发现这种商品单价每降低2元，其销量可增加10件．
（1）求商场经营该商品原来一天可获利润多少元？
（2）设后来该商品每件降价x元，商场一天可获利润y元．
①若商场经营该商品一天要获利润4320元，则每件商品应降价多少元？
②求出y与x之间的函数关系式，当x取何值时，商场获利润最大？并求最大利润值．
如图，已知一次函数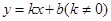
的图象与反比例函数
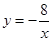的图象交于A，B两点，且A点的横坐标与B点的纵坐标都是-2；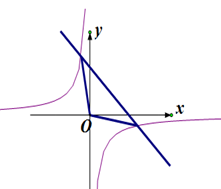
（1）求一次函数的解析式
（2）求△AOB的面积．