如图，在平面直角坐标系中，抛物线
与x轴的右交点为点A，与y
轴的
交点为点B，过点B作x轴的平行线BC，交抛物线于点C，连结AC．现有两动点P，Q分别从O，C两点同时出发，点P以每秒4个单位的速度沿OA向终点A移动，点Q以每秒1个单位的速度沿CB向点B移动，点P停止运动时，点Q也同时停止运动，线段OC，PQ相交于点D，过点D作DE∥OA，交CA于点E，射线QE交x轴于点F．设动点P，Q移动的时间为t（单位:秒）
（1）求A，B，C三点的坐标和抛物线的顶点的坐标；
（2）当t为何值时，四边形PQCA为平行四边形?
（3）请说明当0＜t＜4.5时，△PQF的面积总为定值；
（4）当0≤t≤4.5是否存在△PQF为等腰三角形？当t为何值时，△PQF为等腰三角形?（直接写出结果）
如图：BD平分∠ABC,F在AB上，G在AC上，FC与BD相交于点H.
，
求证：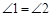 
.
已知如图：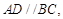
E、F分别在DC、AB延长线上.
,
,
.
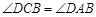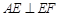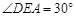（1）求证：DC//AB.
（2）求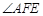
的大小.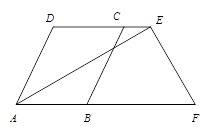
数学课老师提出这样一个问题：已知如图，直线AB//CD,直线EF与直线AB交于G,与直线CD交于H，且GN平分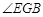
,求证：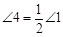
.
下面是某同学给出一种证法，请你将解答中缺少的条件、结论或证明理由补充完整.
证明：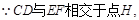
（已知）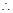
(_________________________)
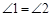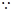AB//CD,EF与AB、CD分别交于G、H(已知)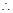
( __________________________ )
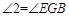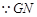是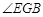的平分线，(已知)
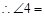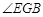_______(角平分线定义)
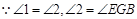(已证)
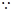（_________________）_______________________(已证)
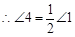(等量代换)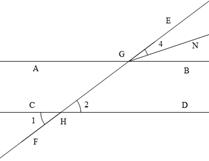
在正方形网格中，每个小正方形的边长均为1个单位长度.
三个顶点的位置如图所示，将点
平移到
,点
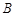平移到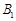
，点C平移到
.
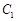(1)请画出平移后的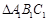
,并写出点B经过怎样的平移得到？
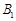(2) 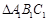的面积是____________.
(3)连接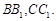
则这两条线段的数量关系是 __________.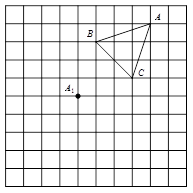
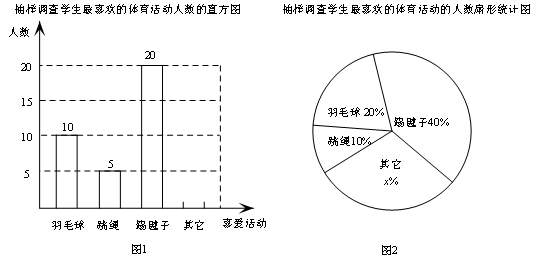
为了解同学对体育活动的喜爱情况，某校设计了“你最喜欢的体育活动是哪一项（仅限一项）”的调查问卷.该校对本校学生进行随机抽样调查，以下是根据调查数据得到的统计图的一部分.请根据以上信息解答以下问题：
(1)该校对多少名学生进行了抽样调查？
(2) ①请补全图1并标上数据 ②图2中x =______.
(3)若该校共有学生900人，请你估计该校最喜欢跳绳项目的学生约有多少人？