为庆祝建党90周年，某校团委计划在七·一前夕举行唱响红歌班级-优题课

为庆祝建党90周年，某校团委计划在“七·一”前夕举行“唱响红歌”班级歌咏比赛，要确定一首喜欢人数最多的歌曲为每班必唱歌曲。为此提供代号为A、B、C、D四首备选曲目让学生选择，经过抽样调查，并将采集的数据绘制如下两幅不完整的统计图。请根据图①，图②所提供的信息，解答下列问题：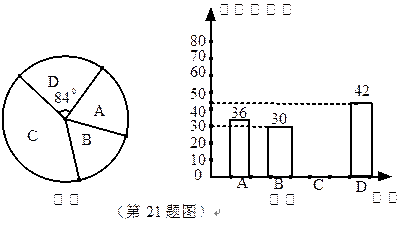
﹪
,
（1）本次抽样调查的学生有_________名，其中选择曲目代号为A的学生占抽样总数的百分比是________%；
（2）请将图②补充完整；
（3）若该校共有1200名学生，根据抽样调查的结果估计全校共有多少名学生选择此必唱歌曲？（要有解答过程）

科目数学题型计算题难度未知

操作：“如图1， $P$ 是平面直角坐标系中一点 $(x$ 轴上的点除外），过点 $P$ 作 $PC ⊥ x$ 轴于点 $C$ ，点 $C$ 绕点 $P$ 逆时针旋转 $60 °$ 得到点 $Q$ ．”我们将此由点 $P$ 得到点 $Q$ 的操作称为点的 $T$ 变换．

（1）点 $P (a, b)$ 经过 $T$ 变换后得到的点 $Q$ 的坐标为　　；若点 $M$ 经过 $T$ 变换后得到点 $N (6, - \sqrt{3})$ ，则点 $M$ 的坐标为　　．

（2） $A$ 是函数 $y = \frac{\sqrt{3}}{2} x$ 图象上异于原点 $O$ 的任意一点，经过 $T$ 变换后得到点 $B$ ．

①求经过点 $O$ ，点 $B$ 的直线的函数表达式；

②如图2，直线 $AB$ 交 $y$ 轴于点 $D$ ，求 $ΔOAB$ 的面积与 $ΔOAD$ 的面积之比．

（1）解不等式组： $\{\begin{matrix} 2 x + 3 > 1 ① \\ x - 2 ⩽ \frac{1}{2} (x + 2) ② \end{matrix}$

（2）解方程： $\frac{5}{2 x - 1} = \frac{3}{x + 2}$ ．

计算：

（1） $| - 6 | + {(- 2)}^{3} + {(\sqrt{7})}^{0}$ ；

（2） $(a + b) (a - b) - a (a - b)$

在平面直角坐标系中，已知 $A (1, 4)$ 、 $B (4, 1)$ 、 $C (m, 0)$ 、 $D (0, n)$ ．

（1）四边形 $ABCD$ 的周长的最小值为　　，此时四边形 $ABCD$ 的形状为　　；

（2）在（1）的情况下， $P$ 为 $AB$ 的中点， $E$ 为 $AD$ 上一动点，连接 $PE$ ，作 $PF ⊥ PE$ 交四边形的边于点 $F$ ，在点 $E$ 从 $D$ 运动到 $A$ 的过程中：

①求 $\tan ∠ PEF$ 的值；

②若 $EF$ 的中点为 $Q$ ，在整个运动过程中，请直接写出点 $Q$ 所经过的路线长．

如图，在平面直角坐标系中，已知点 $A (5, 0)$ ，以原点 $O$ 为圆心、3为半径作圆． $P$ 从点 $O$ 出发，以每秒1个单位的速度沿 $y$ 轴正半轴运动，运动时间为 $t (s)$ ．连接 $AP$ ，将 $ΔOAP$ 沿 $AP$ 翻折，得到 $ΔAPQ$ ．求 $ΔAPQ$ 有一边所在直线与 $⊙ O$ 相切时 $t$ 的值．

试卷网试题网古诗词网作文网范文网