如图，抛物线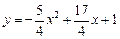
与y轴交于A点，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C(3，0).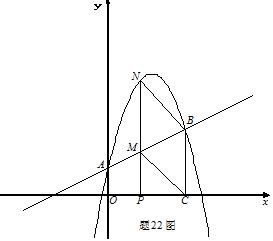
（1）求直线AB的函数关系式；
（2）动点P在线段OC上从原点出发以每秒一个单位的速度向C移动，过点P作PN⊥x轴，交直线AB于点M，交抛物线于点N. 设点P移动的时间为t秒，MN的长度为s个单位，求s与t的函数关系式，并写出t的取值范围；
（3）设在（2）的条件下（不考虑点P与点O，点C重合的情况），连接CM，BN，当t为何值时，四边形BCMN为平行四边形？问对于所求的t值，平行四边形BCMN是否菱形？请说明理由.
已知⊙O的直径为10，点P到点O的距离大于8，那么点P的位置（）
| A．一定在⊙O的内部 |
| B．一定在⊙O的外部 |
| C．一定在⊙O的上 |
| D．不能确定 |
如图，△ABC中，AB＝AC＝10 cm，BD⊥AC于点D，且BD＝6 cm，动点P从点B出发，以1 cm/s的速度，沿B→A的方向运动，到达点A时停止，动点Q从点A出发，以2cm/s的速度，沿A→C的方向运动，到达点C时停止，P、Q两点同时出发，设运动的时间为t （s），△APQ的面积为S（cm2），则S关于t的函数图象大致为（）
如图，△ABC中，AE交BC于点D，∠C =∠E，AD：DE = 3：5，AE=8，BD=4，则DC的长等于（）
A． |
B． |
C． |
D． |
函数
的图象上有两点
，
，若
，则下列结论正确的是（）
A． |
B． |
C． |
D． 、 的大小不确定 |
将抛物线
的图象向右平移2个单位，再向下平移3个单位，得到的抛物线是（）
A． |
B． |
C． |
D． |