 证明以下命题:
证明以下命题:
(Ⅰ)对任一正整a,都存在整数b,c(b<c),使得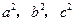 成等差数列。
成等差数列。
(Ⅱ)存在无穷多个互不相似的三角形△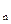 ,其边长
,其边长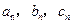 为正整数且
为正整数且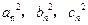 成等差数列。
成等差数列。
已知函数f(x)=ax4lnx+bx4﹣c(x>0)在x=1处取得极值﹣3﹣c,其中a,b,c为常数.
(1)试确定a,b的值;
(2)讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式f(x)≥﹣2c2恒成立,求c的取值范围.
直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=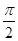 .
.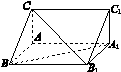
(1)证明:CB1⊥BA1;
(2)已知AB=2,BC=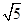 ,求三棱锥C1-ABA1的体积.
,求三棱锥C1-ABA1的体积.
已知向量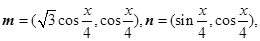 函数
函数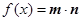 .
.
(1)求函数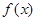 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)在锐角三角形ABC中,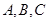 的对边分别是
的对边分别是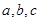 ,且满足
,且满足 求
求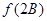 的取值范围.
的取值范围.
设数列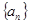 的各项都是正数,且对任意
的各项都是正数,且对任意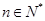 ,都有
,都有 ,其中
,其中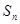 为数列
为数列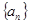 的前
的前 项和。
项和。
(1)求证数列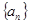 是等差数列;
是等差数列;
(2)若数列 的前
的前 项和为Tn,求Tn。
项和为Tn,求Tn。
在 中,边
中,边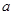 、
、 、
、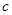 分别是角
分别是角 、
、 、
、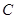 的对边,且满足
的对边,且满足 .
.
(1)求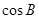 ;
;
(2)若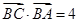 ,
,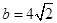 ,求边
,求边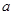 ,
,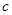 的值.
的值.