(理)在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC
⊥平面ABC,SA=SC=2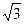 ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
(Ⅰ)证明:AC⊥SB;
(Ⅱ)求二面角N-CM-B的大小;
(Ⅲ)求点B到平面CMN的距离.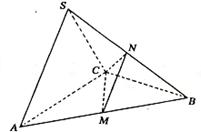
选修4-4:坐标系与参数方程
已知直线 的参数方程是
的参数方程是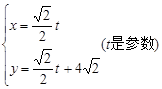 ,圆C的极坐标方程为
,圆C的极坐标方程为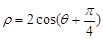 .
.
(1)求圆心C的直角坐标;
(2)由直线 上的点向圆C引切线,求切线长的最小值.
上的点向圆C引切线,求切线长的最小值.
选修4—1:几何证明选讲
如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(1)求AC的长;
(2)求证:BE=EF.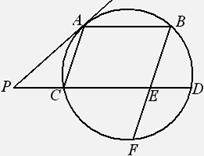
(本小题满分12分)
已知函数f(x)是定义在[-e,0)∪(0,e]上的奇函数,当x∈(0,e],f(x)=ax+lnx(其中e是自然对数的底数,a∈R)
(1)求f(x)的解析式;
(2)设g(x)= ,x∈[-e,0),求证:当a=-1时,f(x)>g(x)+
,x∈[-e,0),求证:当a=-1时,f(x)>g(x)+ ;
;
(3)是否存在实数a,使得当x∈[-e,0)时f(x)的最小值是3 如果存在,求出实数a的值;如果不存在,请说明理由.
(本小题满分12分)
一个四棱锥P-ABCD的正视图是边长为2的正方形及其一条对角线,侧视图和俯视图全全等的等腰直角三角形,直角边长为2,直观图如图.
(1)求四棱锥P-ABCD的体积:
(2)求直线PC和面PAB所成线面角的余弦值;
(3)M为棱PB上的一点,当PM长为何值时,CM⊥PA?
已知数列 ,设
,设 ,数列
,数列 。
。
(1)求证: 是等差数列; (2)求数列
是等差数列; (2)求数列 的前n项和Sn.
的前n项和Sn.