某储运站现有甲种货物1530吨,乙种货物1150吨,安排用一列货车将这批货物运往外地,这列货车持A、B两种类型的货厢共50节。已知甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢,问:该储运站需配置A、B两种类型的货厢各几节?
某校初二年级全体320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不及格”、“及格”、“优秀”三个等级,为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示,试结合图形信息回答下列问题:
(1)这32名学生培训前考分的中位数所在的等级是_______,培训后考分的中位数所在的等级是________.
(2)这32名学生经过培训,考分等级“不合格”的百分比由_________下降到__________.
(3)估计该校整个初二年级中,培训后考分等级为“合格”与“优秀”的学生共有________名
(4)你认为上述估计合理吗?理由是什么?
答:__________ ,
理由为______________________.
我们知道:平均数,中位数和众数都是数据的代表,它们从不同侧面反映了数据的平均水平.有一次:小王、小李和小张三位同学举行射击比赛,每人打10发子弹,命中环数如下:
小王:9 7 6 9 9 10 8 8 7 10
小李:7 10 9 8 9 10 6 8 9 10
小张:10 8 9 10 7 8 9 9 10 10
某种统计结果表明,三人的“平均水平”都是9环.根据这一结果,请判断三人运用了平均数、中位数和众数中的哪一种“平均水平”?(每人写出一个“平均水平”即可)
某市部分学生参加了2005年全国初中数学竞赛决赛,并取得优异成绩,已知竞赛成绩都是整数,试题满分为140分,参赛学生的成绩分布情况如下:
根据以上信息解答下列问题:
(1)全市共有多少人参加本次数学竞赛决赛?最低分和最高分在什么范围内?
(2)经竞赛组委会评定,竞赛成绩在60分以上(含60分)的考生均可获得不同等级的奖励,求此次参加本次竞赛决赛考生的获奖比例;
(3)决赛成绩的中位数落在哪个分数段内?
(4)上表还提供了其他信息,例如:“没获奖的人数为105人”等等,请你再写出两条此表提供的信息。
某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
| 测试项目 |
测试成绩 |
||
| 甲 |
乙 |
丙 |
|
| 教学能力 |
85 |
73 |
73 |
| 科研能力 |
70 |
71 |
65 |
| 组织能力 |
64 |
72 |
84 |
(1)如果根据三项测试的平均成绩,谁将被录用,说明理由;
(2)根据实际需要,学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩,谁将被录用,说明理由.
为了帮助四川灾区学生重返课堂,某市团委发起了“爱心储蓄”活动,鼓励学生将自己的压岁钱和零花钱存入银行,定期一年,到期后可取回本金,而把利息捐给灾区学生. 某校所有同学全都积极参加了这一活动,为灾区同学献一份爱心. 该校学生会根据本校这次活动绘制了如下统计图.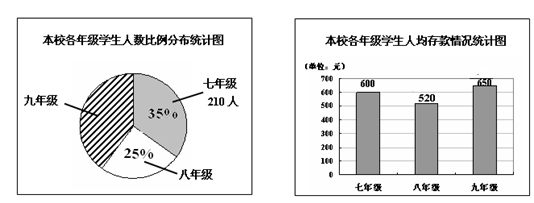
请根据统计图中的信息,回答下列问题:
(1)该校一共有多少名学生?
(2)该校学生人均存款多少元?
(3)已知银行一年期定期存款的年利率是2.25% ,若一名灾区学生一年学习用品的基本费用是400元,那么该校一年大约能为多少名灾区学生提供此项费用?(利息=本金×利率,免收利息税)