(本题8分)为推进阳光体育活动的开展,某校九年级三班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组.经调查,全班同学全员参与,各活动小组人数分布情况的扇形图和条形图如下: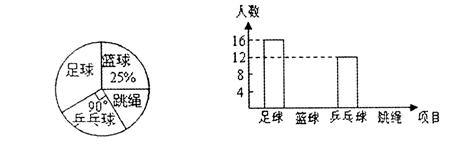
(1)求该班学生人数;
(2)请你补上条形图的空缺部分;
(3)求跳绳人数所占扇形圆心角的大小.
某超市上月销售一种优质新米,平均售价为10元/千克,月销售量为1000千克。经市场调查,若将该种新米价格调低至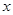 元/千克,则本月销售量
元/千克,则本月销售量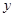 (千克)与
(千克)与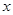 (元/千克)之间满足
(元/千克)之间满足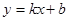 ,且当
,且当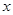 =7时,
=7时,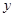 =2000;当
=2000;当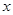 =5时,
=5时,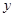 =4000.
=4000.
(1)求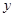 与
与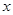 之间的函数关系式。
之间的函数关系式。
(2)已知该种新米上月的进价为5元/千克,本月的进价为4元/千克,要使本月销售该种新米获利比上月增加20%,同时又要让顾客得到实惠,则该种新米的价格应定为多少元?
某商厦九月份的销售额为200万元,十月份的销售额下降了20%,商厦从十一月份起加强管理,改善经营,使销售额稳步上升,十二月份的销售额达到了193.6万元,求这两个月的平均增长率
如图,在⊙0中,AD=BC求证:AB=CD.
已知在Rt△ABC,AB=AC,∠BAC=90°,过A的任一条直线AN,BD⊥AN于D,CE⊥AN于E。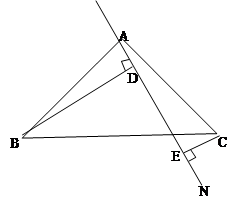
(1)求证:DE=BD-CE
(2)如将直线AN绕A点沿顺时针方向旋转,使它不经过△ABC的内部,再作BD⊥AN于D,CE⊥AN于E,那么DE、DB、CE之间存在等量关系吗?若存在,请证明你的结论?
已知:点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.
求证:(1)△ABC≌△DEF (2)BE=CF.