（本小题8分）为贯彻落实云南省教育厅提出的“三生教育”，在母亲节来临之际，某校团委组织了以“珍爱生命，学会生存，感恩父母”为主题的教育活动，在学校随机调查了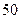
名同学平均每周在家做家务的时间，统计并制作了如下的频数分布和扇形统计图：
根据上述信息回答下列问题：
，
；
在扇形统计图中，
组所占圆心角的度数为 ；
全校共有
名学生，估计该校平均每周做家务时间不少于
小时的学生约有多少人？
如图，在平面直角坐标系中，点A在y轴上，点B在x轴上，C是线段AB的中点，连接OC，并过点A作OC的垂线，垂足为D，交x轴于点E，已知tan∠OAD=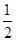
．
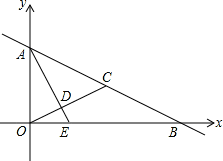
（1）求2∠OAD的正切值；
（2）若OC=
．
①求直线AB的解析式；
②求点D的坐标．
如图，已知正方形ABCD，E是AB延长线上一点，F是DC延长线上一点，连接BF、EF，恰有BF=EF，将线段EF绕点F顺时针旋转90°得FG，过点B作EF的垂线，交EF于点M，交DA的延长线于点N，连接NG．
（1）求证：BE=2CF；
（2）试猜想四边形BFGN是什么特殊的四边形，并对你的猜想加以证明．
某校为了选拔省教委组织的以“爱我省会•让节能环保称为时尚”为主题的参赛作品，现在本校组织了一次“以爱我家乡•让节能环保成为时尚”的作品征集活动，现从所收集上来的作品中随机爱抽取了一部分，按A，B，C，D四个等级进行评选，并根据评选结果绘制了如图所示的条形统计图，已知等级C的作品的所抽取作品中占25%．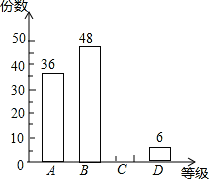
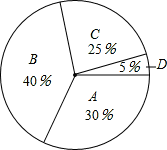
（1）求所抽取的作品的总份数及等级C的作品的份数，并补全条形统计图；
（2）若该校供征集到800份作品．
①请你估计出等级为A的作品约有多少份？
②若等级为A的作品中有100份是七年级组的作品，剩下的为八、九年级组的作品，现要将这两个组的作品再进行分组来选择参赛用的作品，已知这两个组所分的组数相同，且七年级组中每组的作品比八、九年级组中每组的作品少4份，请问这两个年级组的作品中每组各多少份？
已知△ABC中的∠A与∠B满足（1-tanA）2+|sinB-
|=0
（1）试判断△ABC的形状．
（2）求（1+sinA）2-2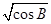
-（3+tanC）0的值．
已知：如图①，在矩形ABCD中，AB=5，AD=
，AE⊥BD，垂足是E．点F是点E关于AB的对称点，连接AF、BF．
（1）求AE和BE的长；
（2）若将△ABF沿着射线BD方向平移，设平移的距离为m（平移距离指点B沿BD方向所经过的线段长度）．当点F分别平移到线段AB、AD上时，直接写出相应的m的值．
（3）如图②，将△ABF绕点B顺时针旋转一个角α（0°＜α＜180°），记旋转中的△ABF为△A′BF′，在旋转过程中，设A′F′所在的直线与直线AD交于点P，与直线BD交于点Q．是否存在这样的P、Q两点，使△DPQ为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由．