如图所示，两条平行的光滑金属导轨固定在倾角为的绝缘斜面上，导轨上端连接一个定值电阻。导体棒和放在导轨上，与导轨垂直开良好接触。斜面上水平虚线以下区域内，存在着垂直穿过斜面向上的匀强磁场。现对棒施以平行导轨斜向上的拉力，使它沿导轨匀速向上运动，此时放在导轨下端的棒恰好静止。当棒运动到磁场的上边界处时，撤去拉力，棒将继续沿导轨向上运动一小段距离后再向下滑动，此时b棒已滑离导轨。当棒再次滑回到磁场上边界处时，又恰能沿导轨匀速向下运动。已知棒、棒和定值电阻的阻值均为，棒的质量为，重力加速度为，导轨电阻不计。求
（1）棒在磁场中沿导轨向上运动的过程中，棒中的电流强度与定值电阻中的电流强度之比；
（2）棒质量；
（3）棒在磁场中沿导轨向上运动时所受的拉力。
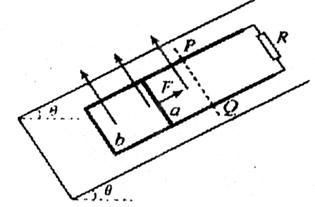
用电动机带动半径为r=0.5m的传输轮来传送一块长方体铁板，放在光滑水平面上的铁板在传输轮的带动下从静止开始向右运动。已知铁板长L=1.6m、质量m=100kg，传输轮与铁板间的动摩擦因子μ=0.1。工作时传输轮对铁板产生竖直向下、大小为50N的恒定压力，传输轮转动的角速度恒为ω=1rad/s，g取10m/s2。求：
（1）传输轮对铁板的摩擦力大小；
（2）铁板离开传输轮时的速度大小。
如图12所示，A，B，C为某匀强电场中的三点，已知：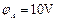
，
，
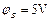，试在该虚线框内作出该电场的示意图，（画出几条电场线），并要求保留作图时所用的辅助线，若将一个电子从A点移到B点，电场力做功多少电子伏？
如图所示，在纸平面内建立如图所示的直角坐标系xoy，在第一象限的区域存在沿y轴正方向的匀强电场。现有一质量为m、电量为e的电子从第一象限的某点P（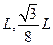
）以初速度v0沿x轴的负方向开始运动，经过
轴上的点Q（
）进入第四象限，先做匀速直线运动然后进入垂直纸面的矩形匀强磁场区域，其左边界和上边界分别与y轴、x轴重合，电子经磁场偏转后恰好经过坐标原点O并沿y轴的正方向运动，不计电子的重力。求
（1）电子经过Q点的速度
；
（2）该匀强磁场的磁感应强度
；
（3）该匀强磁场的最小面积S。
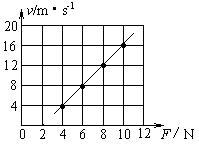
水平面上两根足够长的金属导轨平行固定放置，间距为L，一端通过导线与阻值为R的电阻连接；导轨上放一质量为m的金属杆（见图），金属杆与导轨的电阻忽略不计；均匀磁场竖直向下。用与导轨平行的恒定拉力F作用在金属杆上，杆最终将做匀速运动。当改变拉力的大小时，相对应的匀速运动速度v也会变化，v与F的关系如右下图。（取重力加速度g=10m/s2）
（1）金属杆在匀速运动之前做什么运动？
（2）若m=0．5kg，L=0．5m，R=0．5Ω；磁感应强度B为多大？
（3）由v—F图线的截距可求得什么物理量？其值为多少？
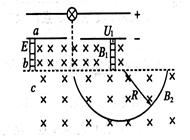
质谱仪原理如图，a为粒子加速器电压为u1，b为速度选择器，磁场与电场正交，磁感强度为B1，板间距离为d，c为偏转分离器，磁感强度为B2，今有一质量为m，电量为+e的电子（不计重力），经加速后，该离子恰能通过速度选择器，粒子进入分离器后做匀速圆周运动，求：
（1）粒子的速率v
（2）速度选择器的电压u2
（3）粒子在B2的磁场中做匀速圆周运动的半径R