如图所示,质量的滑块套在光滑的水平轨道上,质量的小球通过长的轻质细杆与滑块上的光滑轴连接,小球和轻杆可在竖直平面内绕轴自由转动,开始轻杆处于水平状态,现给小球一个竖直向上的初速度,取。

(1)若锁定滑块,试求小球通过最高点时对轻杆的作用力大小和方向。
(2)若解除对滑块的锁定,试求小球通过最高点时的速度大小。
(3)在满足(2)的条件下,试求小球击中滑块右侧轨道位置点与小球起始位置点间的距离。
法国人劳伦斯·费舍尔在澳大利亚的冒险世界进行高空特技表演,他从20m高的塔上直接落入水池中(可视为自由落体运动)。落入水中可视为匀减速直线运动,加速度大小为a=8m/s2.求:
(1)落入水面时的速度?
(2)需要准备一个至少深度为多少米的水池。(g取10m/s2)
汽车(可视为质点)由静止开始,做加速度为2m/s2匀加速直线运动。通过长为900m的隧道。求:(1)汽车在第3s末的速度大小?
(2)汽车通过隧道所用的时间是多少?
如图所示,以A、B和C、D为端点的半径为R=0.6m的两半圆形光滑绝缘轨道固定于竖直平面内,B端、C端与光滑绝缘水平地面平滑连接。A端、D端之间放一绝缘水平传送带。传送带下方B、C之间的区域存在水平向右的匀强电场,场强E=5×105V/m。当传送带以6m/s的速度沿图示方向匀速运动时,现将质量为m=4×10-3kg,带电量q=+1×10-8C的物块从传送带的右端由静止放上传送带。小物块运动第一次到A时刚好能沿半圆轨道滑下。不计小物块大小及传送带与半圆轨道间的距离,g取10m/s2,已知A、D端之间的距离为1.2m。求:
(1)物块与传送带间的动摩擦因数;
(2)物块第1次经CD半圆形轨道到达D点时速度;
(3)物块第几次经CD半圆形轨道到达D点时的速度达到最大,最大速度为多大。
如图所示的装置,U1是加速电压,紧靠其右侧的是两块彼此平行的水平金属板,板长为L,两板间距离为d。一个质量为m,带电量为-q的质点,经加速电压加速后沿两金属板中心线以速度v0水平射入两板中。若在两水平金属板间加一电压U2,当上板为正时,带电质点恰能沿两板中心线射出;当下板为正时,带电质点则射到下板上距板的左端L/4处,为使带电质点经U1加速后沿中心线射入两金属板,并能够从两金属之间射出,问:两水平金属板间所加电压应满足什么条件.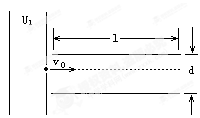
如图所示,在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC,其下端(C端)距地面高度h=0.8 m.有一质量为500 g的带电小环套在直杆上,正以某一速度沿杆匀速下滑.小球离杆后正好通过C端的正下方P点处.(g取10 m/s2)求: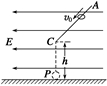
(1)小环离开直杆后运动的加速度大小和方向;
(2)小环从C运动到P过程中的动能增量;
(3)小环在直杆上匀速运动时速度的大小v0.