如图,定点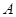 和
和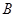 都在平面
都在平面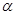 内,定点
内,定点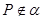 ,
,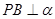 ,
, 是
是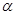 内异于
内异于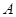 和
和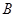 的动点,且
的动点,且 ,那么动点
,那么动点 在平面
在平面 内的轨迹是( )
内的轨迹是( )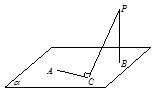
 一条直线,但去掉两个点
一条直线,但去掉两个点 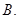 一个圆,但去掉两个点
一个圆,但去掉两个点 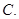 一个圆
一个圆 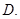 半个圆,但去掉两个点
半个圆,但去掉两个点
已知偶函数 满足条件:当
满足条件:当 时,恒有
时,恒有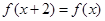 ,且
,且 时,有
时,有  则
则 的大小关系为()
的大小关系为()
A. |
B. |
C. |
D. |
当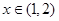 时,不等式
时,不等式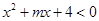 恒成立,则
恒成立,则 的取值范围为()
的取值范围为()
A.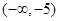 |
B.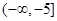 |
C.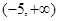 |
D.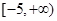 |
设函数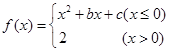 ,若
,若 ,则关于
,则关于 的方程
的方程 的解的个数为()
的解的个数为()
| A.0 | B.1 | C.2 | D.3 |
下列关于函数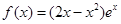 的判断:
的判断:
①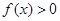 的解集是
的解集是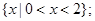 ②
②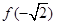 是极小值,
是极小值,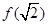 是极大值;
是极大值;
③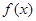 没有最小值,也没有最大值.其中判断正确的命题个数为()
没有最小值,也没有最大值.其中判断正确的命题个数为()
| A.0 | B.1 | C.2 | D.3 |
下列推理:
①由 为两个不同的定点,动点
为两个不同的定点,动点 满足
满足 ,得点
,得点 的轨迹为双曲线
的轨迹为双曲线
②由 ,求出
,求出 猜想出数列
猜想出数列 的前
的前 项和
项和 的表达式
的表达式
③由圆 的面积
的面积 ,猜想出椭圆
,猜想出椭圆 =1的面积
=1的面积
④科学家利用鱼的沉浮原理制造潜艇。其中是归纳推理的命题个数为()
| A.0 | B.1 | C.2 | D.3 |