(本小题满分13分)设 (
(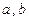 为实常数)。
为实常数)。
(1)当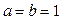 时,证明:
时,证明: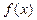 不是奇函数;
不是奇函数;
(2)设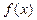 是奇函数,求
是奇函数,求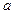 与
与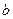 的值;
的值;
(3)求(2)中函数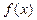 的值域。
的值域。
已知:

通过观察上述两等式的规律,请你写出一般性的命题,并给出的证明.
已知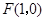 ,直线
,直线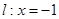 ,
,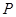 为平面上的动点,过点
为平面上的动点,过点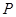 作
作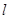 的垂线,垂足为点
的垂线,垂足为点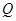 ,且
,且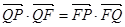 .
.
(Ⅰ)求动点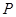 的轨迹曲线
的轨迹曲线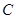 的方程;
的方程;
(Ⅱ)设动直线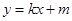 与曲线
与曲线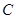 相切于点
相切于点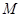 ,且与直线
,且与直线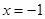 相交于点
相交于点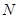 ,试问:在
,试问:在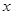 轴上是否存在一个定点
轴上是否存在一个定点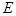 ,使得以
,使得以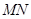 为直径的圆恒过此定点
为直径的圆恒过此定点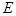 ?若存在,求出定点
?若存在,求出定点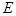 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
已知函数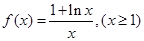 .
.
(Ⅰ)试判断函数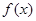 的单调性,并说明理由;
的单调性,并说明理由;
(Ⅱ)若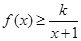 恒成立,求实数
恒成立,求实数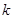 的取值范围.
的取值范围.
如图,已知空间四边形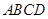 中,
中,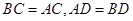 ,
,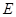 是
是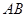 的中点.
的中点. 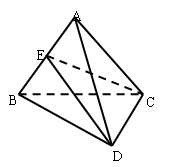
(Ⅰ)求证: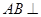 平面CDE;
平面CDE;
(Ⅱ)若G为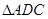 的重心,试在线段AE上确定一点F,使得GF//平面CDE.
的重心,试在线段AE上确定一点F,使得GF//平面CDE.
口袋中有5个大小相同的小球,其中1个小球标有数字“3”,2个小球标有数字“2”,2个小球标有数字“1”,每次从中任取一个小球,取后不放回,连续抽取两次。
(I)求两次取出的小球所标数字不同的概率;
(II)记两次取出的小球所标数字之和为X,求事件 的概率。
的概率。