已知对任意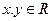 ,都有
,都有 (
(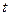 为常数)并且当
为常数)并且当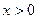 时,
时,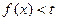
⑴ 求证: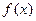 是R上的减函数;
是R上的减函数;
⑵ 若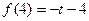 , 解关于m的不等式
, 解关于m的不等式 。
。
如图3-2,设有一个等边三角形网格,其中每个最小等边三角形的边长都是 cm,现用直径等于2cm的硬币投掷到此网格上,求硬币落下后与格线没有公共点的概率.
cm,现用直径等于2cm的硬币投掷到此网格上,求硬币落下后与格线没有公共点的概率.
图3-2
有两个人在一座11层大楼的底层进入电梯,设他们中的每一个人自第二层开始的每一层离开是等可能的,求两个人在不同层离开的概率.
有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,具体规则如下:
| 规则编号 |
游戏① |
游戏② |
游戏③ |
| 袋子球数 |
1个红球和1个白球 |
2个红球和2个白球 |
3个红球和2个白球 |
| 规则 |
取1个球,取出的球是红球则获奖 |
取2个球,取出的球同色则获奖 |
取2个球,取出的球不同色则获奖 |
每个同学可选择参加两项游戏,请你选择,并说出道理.
向三个相邻的军火库投掷一颗炸弹,炸中第一个军火库的概率为0.025,炸中其余两个军火库的概率都为0.1,只要炸中一个,另外两个也要爆炸,求军火库爆炸的概率.
(1)如图3-3,某人投标投中圆的概率是多少(投在正方形外面或边缘不算)?
(2)同(1)中图形,利用随机模拟的方法近似计算正方形内切圆的面积,并估计π的近似值.
图3-3