为继续进行旅游景区公共服务改造,某市今年预算用资金41万元在200余家A
级景区配备两 种轮椅1100台,其中普通轮椅每台360元,轻便型轮椅每台500元.
种轮椅1100台,其中普通轮椅每台360元,轻便型轮椅每台500元.
(1) 若恰好全部用完预算资金,能购买 两种轮椅各多少台?
两种轮椅各多少台?
(2) 由于获得了不超过4万元的社会捐助,问轻便型轮椅最多可以买多少台?
(南充)如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.
(1)判断△AMP,△BPQ,△CQD和△FDM中有哪几对相似三角形?(不需说明理由)
(2)如果AM=1,sin∠DMF=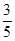 ,求AB的长.
,求AB的长.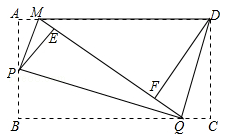
(南充)如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1, ,
, ,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小;
(3)求CQ的长.
(南充)已知抛物线 与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
(1)求抛物线解析式.
(2)直线 (
( )与抛物线相交于两点M(
)与抛物线相交于两点M( ,
, ),N(
),N( ,
, )(
)( ),当
),当 最小时,求抛物线与直线的交点M与N的坐标.
最小时,求抛物线与直线的交点M与N的坐标.
(3)首尾顺次连接点O、B、P、C构成多边形的周长为L,若线段OB在x轴上移动,求L最小值时点O,B移动后的坐标及L的最小值.
(攀枝花)如图1,矩形ABCD的两条边在坐标轴上,点D与坐标原点O重合,且AD=8,AB=6.如图2,矩形ABCD沿OB方向以每秒1个单位长度的速度运动,同时点P从A点出发也以每秒1个单位长度的速度沿矩形ABCD的边AB经过点B向点C运动,当点P到达点C时,矩形ABCD和点P同时停止运动,设点P的运动时间为t秒.
(1)当t=5时,请直接写出点D、点P的坐标;
(2)当点P在线段AB或线段BC上运动时,求出△PBD的面积S关于t的函数关系式,并写出相应t的取值范围;
(3)点P在线段AB或线段BC上运动时,作PE⊥x轴,垂足为点E,当△PEO与△BCD相似时,求出相应的t值.
(巴中)如图,在平面直角坐标系xOy中,二次函数 (
( )的图象与x轴交于A(﹣2,0)、B(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
)的图象与x轴交于A(﹣2,0)、B(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
(1)求该二次函数的解析式;
(2)如图1,连结BC,在线段BC上是否存在点E,使得△CDE为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)如图2,若点P(m,n)是该二次函数图象上的一个动点(其中m>0,n<0),连结PB,PD,BD,求△BDP面积的最大值及此时点P的坐标.