为了了解某区初中学生上学的交通方式,从中随机调查了300 0名学生的上学交通方式,统计结果如图所示.
0名学生的上学交通方式,统计结果如图所示.
(1)补全以上两幅统计图并标注相应数值;
(2)该区共有初中学生15000名,请估计其中骑自行上学的人数.
如图,在△ABC中,AB=AC=10,BC=16,⊙A的半径为7,判断⊙A与直线BC的位置关系,并说明理由.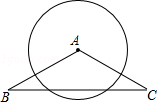
水资源越来越缺乏,全球提倡节约用水,水厂为了了解某小区居民的用水情况,随机抽查了该小区10户家庭的月用水量,有关数据如下表:
| 月用水量(m3) |
10 |
13 |
14 |
17 |
18 |
| 户数 |
2 |
2 |
3 |
2 |
1 |
如果该小区有500户家庭,根据上面的统计结果,估计该小区居民每月需要用水多少立方米?(写出解答过程).
先化简,再求值:[(a-2b)2-(a+2b)(a-2b)]÷4b,其中a=2,b=-1.
如图,已知∠ABD=40°,∠ADB=65°,AB∥DC,求∠ADC的度数.
在如图的平面直角坐标系中,已知点A(-2,-1),B(0,-3),C(1,-2),请在如图上画出△ABC和与△ABC关于x轴对称的△A1B1C1.