如图，边长为4的正方形OABC的顶点O为坐标原点，点A
在x轴的正半轴上，点C在y轴的正半轴上．动点D在线段BC上移动（不与B，C重合），
连接OD，过点D作DE⊥OD，交边AB于点E，连接OE。
（1）当CD=1时，求点E的坐标；
（2）如果设CD=t，梯形COEB的面积为S，那么是否存在S的最大值？若存在，请求出这
个最大值及此时t的值；若不存在，请说明理由。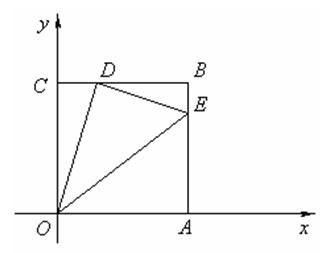
我们学习了因式分解之后可以解某些高次方程．例如，一元二次方程x2 + x − 2 = 0可以通过因式分解化为：(x − 1) (x + 2) = 0，则方程的两个解为x = 1和x = −2．反之，如果x = 1是某方程ax2 + bx + c = 0的一个解，则多项式ax2 + bx + c必有一个因式是(x − 1)．
在理解上文的基础上，试找出多项式x3 + x2 − 3x + 1的一个因式，并将这个多项式因式分解．
如图，已知△ABC中，AD是高，AE是角平分线．
(1)若∠B=20°，∠C=60°，则∠EAD=_______°；
(2)若∠B=a°，∠C=b°（b＞a），试通过计算，用a、b的代数式表示∠EAD的度数；
(3)特别地，当△ABC为等腰三角形（即∠B=∠C）时，请用一句话概括此时AD和AE的位置关系：____．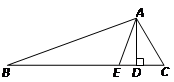
从三个多项式：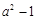
，
，
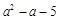中选择适当的两个进行加法运算，并把结果因式分解．
在下列解题过程的空白处填上适当的内容（推理的理由或数学表达式）
如图，已知AB∥CD，BE、CF分别平分∠ABC和∠DCB，求证：BE∥CF．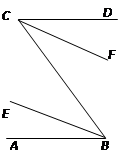
证明：
∵AB∥CD，（已知）
∴∠_____=∠_____．（）
∵，（已知）
∴∠EBC=
∠ABC．（角的平分线定义）
同理，∠FCB=．
∴∠EBC=∠FCB．（等式性质）
∴BE∥CF．（）
化简求值：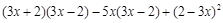
，其中
．