如图，在梯形ABCD中，AD∥BC，∠B是直角，AB＝14 cm，AD＝18 cm．BC＝21 cm，点P从点A出发，沿边AD向点D以1 cm/s的速度移动，点Q从点C出发沿边CB向点B以9cm/s的速度移动，若有一点运动到端点时，另一点也随之停止．如果P、Q同时出发，能否有四边形PQCD成等腰梯形？如果存在，求经过几秒后四边形PQCD成等腰梯形；如果不存在，请说明理由．(本题9分)
某超市用3000元购进某种干果销售，由于销售状况良好，超市又调拨9000元资金购进该种干果，但这次的进价比第一次的进价提高了20%，购进干果数量是第一次的2倍还多300千克．
（1）该种干果的第一次进价是每千克多少元？
（2）如果超市按每千克9元的价格出售，当大部分干果售出后，余下的600千克按售价的8折售完，超市销售这种干果共盈利多少元？
小明遇到这样一个问题：如图1，在Rt△ABC中，∠ACB=90°，∠A=60°，CD平分∠ACB，试判断BC和AC、AD之间的数量关系．小明发现，利用轴对称做一个变化，在BC上截取CA′=CA，连接DA′，得到一对全等的三角形，从而将问题解决（如图2）．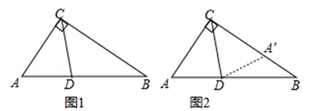
（1）求证：△ADC≌△A′DC；
（2）试猜想写出BC和AC、AD之间的数量关系，并给出证明．
解分式方程：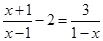
．
计算：（1）
；
（2）化简：
．
如图，在平面直角坐标系中完成下列各题：（不写作法，保留作图痕迹）
（1）在图1中作出
关于y轴对称的
，并写出
、
、
的坐标；
（2）在图2中x轴上画出点
，使
的值最小．