(本小题满分14分)
设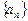 为等差数列,
为等差数列, 为数列
为数列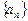 的前
的前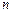 项和,已知
项和,已知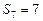 ,
, .
.
(Ⅰ)求数列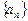 的通项公式;
的通项公式;
(Ⅱ)若 ,求数列
,求数列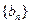 的前
的前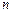 项和
项和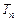 。
。
(本小题满分12分) 中,已知
中,已知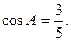
(Ⅰ)求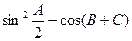 的值;
的值;
(Ⅱ)若 的面积为4,|AB=2,求BC边的长。
的面积为4,|AB=2,求BC边的长。
(本小题满分12分)
函数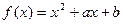 ,不等式
,不等式 的解集为
的解集为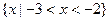
(Ⅰ)求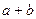 的值;
的值;
(Ⅱ)设函数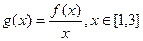 ,求函数
,求函数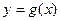 的最小值与对应
的最小值与对应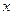 的值。
的值。
(本小题满分10分)
已知某几何体的正视图、侧视图都是直角三角形,俯视图是矩形(尺寸如图所示)。
(I)利用所给提示图,作出该几何体的直观图;
(Ⅱ)求该几何体的体积V。

(本小题满分12分)
已知函数
(I)求函数 处的切线的方程;
处的切线的方程;
(II)设实数
本小题满分12分)
已知抛物线
(I)求p与m的值;
(II)若斜率为—2的直线l与抛物线G交于P、Q两点,点M为抛物线G上一点,其横坐标为1,记直线PM的斜率为k1,直线QM的斜率为k2,试问: 是否为定值?请证明你的结论。
是否为定值?请证明你的结论。