(本小题满分12分)函数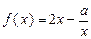 的定义域为
的定义域为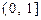 (
(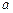 为实数).
为实数).
(1)当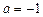 时,求函数
时,求函数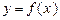 的值域;
的值域;
(2)若函数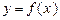 在定义域上是减函数,求
在定义域上是减函数,求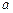 的取值范围;
的取值范围;
(3)函数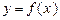 在
在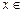
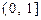 上的最大值及最小值,并求出函数取最值时
上的最大值及最小值,并求出函数取最值时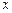 的值.
的值.
设平面直角坐标系 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
(Ⅰ)求实数b 的取值范围;
(Ⅱ)求圆C 的方程;
如图,在正三棱柱ABC—A1B1C1中,底面边长及侧棱长均为2,D是棱AB的中点,
(1)求证 ;
;
(2)求异面直线AC1与B1C所成角的余弦值. 
如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点,求证:平面D1BQ∥平面PAO.
根据下列条件求直线方程
(1)过点(2,1)且倾斜角为 的直线方程;
的直线方程;
(2)过点(-3,2)且在两坐标轴截距相等的直线方程.
(14分)如图①,直角梯形 中,
中, ,点
,点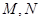 分别在
分别在 上,且
上,且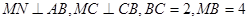 ,现将梯形
,现将梯形 A沿
A沿 折起,使平面
折起,使平面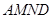 与平面
与平面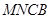 垂直(如图②).
垂直(如图②).
(1)求证: 平面
平面 ;
;
(2)当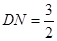 时,求二面角
时,求二面角 的大小.
的大小.