已知二次函数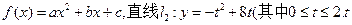
为常数) ;
; .若直线
.若直线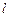 1、
1、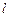 2与函数
2与函数 的图象以及
的图象以及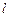 2,y轴与函数
2,y轴与函数 的图象
的图象
所围成的封闭图形如阴影所示.
(1)求
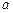 、b、c的值;
、b、c的值;
(2)求阴影面积S关于t的函数S(t)的解析式;
(3)若 问是否存在实数m,使得
问是否存在实数m,使得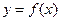 的图象与
的图象与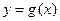 的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
已知四棱锥 ,其中
,其中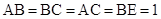 ,
, ,
,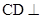 面
面 ,
,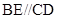 ,
, 为
为 的中点.
的中点.
(Ⅰ)求证: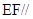 面
面 ;
;
(Ⅱ)求证:面 面
面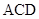 ;
;
(III)求四棱锥 的体积.
的体积.
 的内角
的内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, .向量
.向量 与
与 平行.
平行.
(Ⅰ)求角 ;
;
(Ⅱ)若 ,
, ,求
,求 的面积.
的面积.
某个团购网站为了更好地满足消费者,对在其网站发布的团购产品展开了用户调查,每个用户在使用了团购产品后可以对该产品进行打分,最高分是 分.上个月该网站共卖出了
分.上个月该网站共卖出了 份团购产品,所有用户打分的平均分作为该产品的参考分值,将这些产品按照得分分成以下几组:第一组
份团购产品,所有用户打分的平均分作为该产品的参考分值,将这些产品按照得分分成以下几组:第一组 ,第二组
,第二组 ,第三组
,第三组 ,第四组
,第四组 ,第五组
,第五组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(Ⅰ)分别求第三,四,五组的频率;
(Ⅱ)该网站在得分较高的第三,四,五组中用分层抽样的方法抽取了 个产品作为下个月团购的特惠产品,某人决定在这
个产品作为下个月团购的特惠产品,某人决定在这 个产品中随机抽取
个产品中随机抽取 个购买,求他抽到的两个产品均来自第三组的概率.
个购买,求他抽到的两个产品均来自第三组的概率.
已知抛物线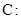
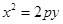 (
( )的焦点为
)的焦点为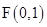 ,过点
,过点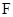 作直线
作直线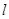 交抛物线
交抛物线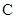 于
于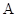 ,
,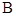 两点.椭圆
两点.椭圆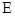 的中心在原点,焦点在
的中心在原点,焦点在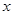 轴上,点
轴上,点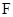 是它的一个顶点,且其离心率
是它的一个顶点,且其离心率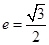 .
.
(Ⅰ)分别求抛物线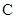 和椭圆
和椭圆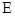 的方程;
的方程;
(Ⅱ)经过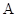 ,
,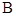 两点分别作抛物线
两点分别作抛物线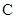 的切线
的切线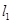 ,
,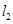 ,切线
,切线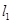 与
与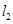 相交于点
相交于点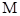 .证明:
.证明: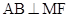 .
.
已知函数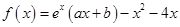 ,曲线
,曲线 在点
在点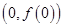 处切线方程为
处切线方程为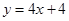 .
.
(1)求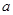 ,
,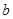 的值;
的值;
(2)讨论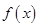 的单调性,并求
的单调性,并求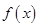 的极大值.
的极大值.