小芸在为班级办黑板报时遇到了一个难题,在版面设计过程中需将一个半圆面三等分,请你帮助她设计一个合理的等分方案.要求用尺规作出图形,保留作图痕迹,并简要写出作法.
(1)计算:(-2)-1-|-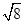 |+(
|+( -1)0+cos45°.
-1)0+cos45°.
(2))已知m2-5m-14=0,求(m-1)(2m-1)-(m+1)2+1的值.
在平面直角坐标系xoy中, 一块含60°角的三角板作如图摆放,斜边AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).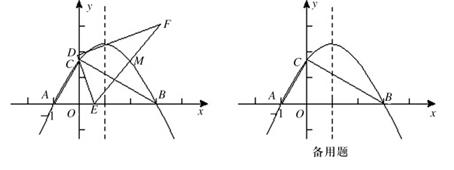
(1)请直接写出点B、C的坐标:B(,)、C(,);并求经过A、B、C三点的抛物线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C.此时,EF所在直线与(1)中的抛物线交于第一象限的点M.
①设AE=x,当x为何值时,△OCE∽△OBC;
②在①被满足的情况下探究:抛物线的对称轴上是否存在点P使△PEM是等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:DF·DE=CE·CB;
(2)若AB=4,AD=3 ,AE=3,求AF的长.
,AE=3,求AF的长.
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数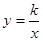 (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=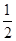 .
.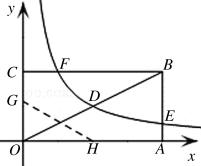
(1)求反比例函数的解析式和n的值;
(2)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
尼泊尔地震牵动着全中国人民的心,中国红十字基金会开展了“一方有难,八方支援”的赈灾活动.5月15日,中国红十字基金会联手北京成龙慈善基金会等共同出资400万元人民币,采购5000只“赈济家庭箱”(“赈济家庭箱”包括当地受灾群众急需的毛毯、防潮垫、睡袋、雨衣、服装、餐具、个人护理用品等),作为首批物资援助尼泊尔地震灾区.该基金会计划到第三批援助物资为止共采购18200只“赈济家庭箱”.
(图为中国红十字基金会工作人员介绍“赈济家庭箱”内的物品)
(1)如果第二批、第三批援助物资的增长率相同,求采购“赈济家庭箱”的增长率.
(2)按照(1)中采购“赈济家庭箱”的增长速度,该基金会采购第四批“赈济家庭箱”需要筹措资金多少万元?