如图，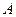
、
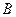两座城市相距100千米，现计划在这两座城市之间修筑一条高等级公路（即线段
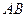）。经测量，森林保护区中心
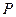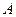点在城市的北偏东30°方向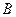，城市的北偏西45°方向上，已知森林保护区的范围在以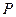为圆心，50千米为半径的圆形区域内。请问：计划修筑的这条高等级公路会不会穿越保护区，为什么？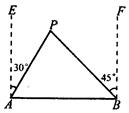
如图，在△ABC中，∠ABC=2∠C，BD平分∠ABC，且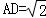
，
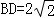，求AB的值．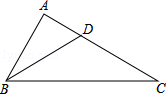
如图△ABC中，DE∥BC，
=
，M为BC上一点，AM交DE于N．
（1）若AE=4，求EC的长；
（2）若M为BC的中点，S△ABC=36，求S△ADN．
现代互联网技术的广泛应用，催生了快递行业的高度发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同．
（1）求该快递公司投递总件数的月平均增长率；
（2）如果平均每人每月最多可投递0.6万件，那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？
已知关于x的方程x2+（m+2）x+2m﹣1=0．
（1）求证：方程有两个不相等的实数根．
（2）若1是该方程的一个根．求m的值并求出此时方程的另一个根．
解方程：
（1）x2﹣8x﹣10=0；
（2）9t2﹣（t﹣1）2=0．