如图所示,将矩形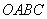 沿
沿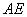 折叠,使点
折叠,使点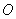 恰好落在
恰好落在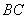 上
上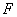 处,以
处,以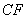 为边作正方形
为边作正方形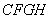 ,延长
,延长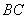 至
至 ,使
,使 ,再以
,再以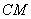 、
、 为边作矩形
为边作矩形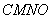 .
.
(1). 试比较 、
、 的大小,并说明理由.
的大小,并说明理由.
2)令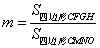 ,请问
,请问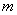 是否为定值?若是,请求出
是否为定值?若是,请求出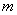 的值;若不是,请说明理由.
的值;若不是,请说明理由.
3在(2)的条件下,若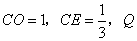 为
为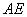 上一点且
上一点且 ,抛物线
,抛物线 经过
经过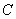 、
、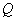 两点,请求出此抛物线的解析式.
两点,请求出此抛物线的解析式.
(4).在(3)的条件下,若抛物线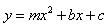 与线段
与线段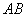 交于点
交于点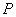 ,试问在直线
,试问在直线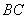 上是否存在点
上是否存在点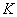 ,使得以
,使得以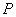 、
、 、
、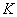 为顶点的三角形与
为顶点的三角形与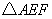 相似?若存在,请求直线
相似?若存在,请求直线 与
与 轴的交点
轴的交点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(﹣6,0),B点坐标为(4,0),点D为BC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点的抛物线的解析式为 .
.
(1)求抛物线的解析式;
(2)如图①,将△BDE以DE为轴翻折,点B的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)如图②,当点E在线段AB上运动时,抛物线 的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A1B1C1.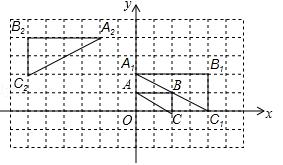
(1)△ABC与△A1B1C1的位似比等于 ;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A1B1C1是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .
如图,已知经过点D(2, )的抛物线
)的抛物线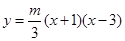 (m为常数,且m>0)与x轴交于点A、B(点A位于B的左侧),与y轴交于点C.
(m为常数,且m>0)与x轴交于点A、B(点A位于B的左侧),与y轴交于点C.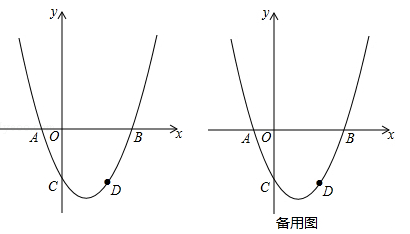
(1)填空:m的值为 ,点A的坐标为 ;
(2)根据下列描述,用尺规完成作图(保留作图痕迹,不写作法):连接AD,在x轴上方作射线AE,使∠BAE=∠BAD,过点D作x轴的垂线交射线AE于点E;
(3)动点M、N分别在射线AB、AE上,求ME+MN的最小值;
(4)t是过点A平行于y轴的直线,P是抛物线上一点,过点P作l的垂线,垂足为点G,请你探究:是否存在点P,使以P、G、A为顶点的三角形与△ABD相似?若存在,求出点P的坐标;若不存在,说明理由.
(·辽宁锦州)如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是 ;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF= AD,请给出证明;
AD,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
(·辽宁锦州)如图,在平面直角坐标系中,线段AB的两个端点是A(﹣5,1),B(﹣2,3),线段CD的两个端点是C(﹣5,﹣1),D(﹣2,﹣3).
(1)线段AB与线段CD关于直线对称,则对称轴是 ;
(2)平移线段AB得到线段A1B1,若点A的对应点A1的坐标为(1,2),画出平移后的线段A1B1,并写出点B1的坐标为 .