阅读下列材料:
解答“已知x-y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解:因为x-y=2,所以x=y+2.
因为x>1,所以y+2>1.
因为y<0,所以-1<y<0.①
同理得1<x<2.②
有①+ ②得-1+1<x+y<0+2,
所以x+y的取值范围是0<x+y<2.
请按照上述方法,完成下列问题:
(1)已知x-y=3,且x>2,y<1,则x+y的取值范围是_____________________。
(2)已知y>1,x<-1,若x-y=a成立,求x+y的取值范围(结果用含a的式子表示)。
如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E。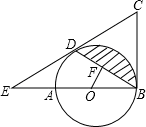
(1)求证:CD为⊙O的切线。
(2)若BD的弦心距OF=1,∠ABD=30度,求图中阴影部分的面积(结果保留∏)。
【课本节选】
反比例函数y=(k为常数,k≠0)的图象是双曲线.当k>0时,双曲线两个分支分别在三象限,在每一个象限内,y随x的增大而减小(简称增减性);反比例函数的图象关于原点对称(简称对称性).这些我们熟悉的性质,可以通过说理得到吗?
【尝试说理】
我们首先对反比例函数y=(k>0)的增减性来进行说理.如图,当x>0时.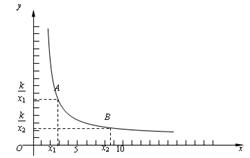
在函数图象上任意取两点A、B,设A(x1,),B(x2,),
且0<x1<x2.
下面只需要比较和的大小.
—=.
∵0<x1<x2,∴x1-x2<0,x1 x2>0,且 k>0.
∴<0.即<.
这说明:x1<x2时,>.也就是:自变量值增大了,对应的函数值反而变小了.
即:当x>0时,y随x的增大而减小.
同理,当x<0时,y随x的增大而减小.
(1)试说明:反比例函数y= (k>0)的图象关于原点对称.
【运用推广】
(2)分别写出二次函数y=ax2(a>0,a为常数)的对称性和增减性,并进行说理.
对称性:;
增减性:.
说理:
(3)对于二次函数y=ax2+bx+c (a>0,a,b,c为常数),请你从增减性的角度,简要解释为何当x=—时函数取得最小值.
问题提出:
平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一直线上),能否在同一个圆呢?
初步思考
设不在同一条直线上的三点A、B、C确定的圆为⊙O.
(1)当C、D在线段AB的同侧时,
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是;
如图②,若点D在⊙O内,此时有∠ACB∠ADB;
如图③,若点D在⊙O外,此时有∠ACB∠ADB.(填“=”、“>”或“<”);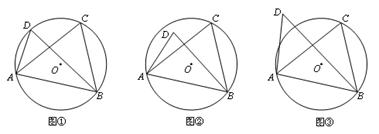
由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件:.
类比学习
(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形.
此时有,此时有, 此时有.
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件:.
拓展延伸
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知:如图,AB是⊙O的直径,点C在⊙O上.
求作:CN⊥AB.
作法:①连接CA,CB;
②在上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M;
⑤连接D、M并延长,交⊙O于N.连接CN.
则CN⊥AB.
请按上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)
如图,在□ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.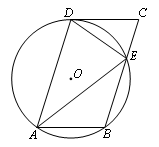
(1)判断四边形ABED的形状,并说明理由;
(2)判断直线DC与⊙O的位置关系,并说明理由;
(3)若AB=3,AE=6,求CE的长.