用代数式表示“ 的3倍与
的3倍与 的平方的差”,正确的是( )
的平方的差”,正确的是( )
A. |
B. |
C. |
D. |
不等式组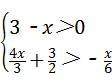 的最小整数解为( )
的最小整数解为( )
| A.0 | B.1 |
| C.2 | D.﹣1 |
如图,边长为6的大 正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的
正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的 值为( )
值为( )
| A.16 | B.17 |
| C.18 | D.19 |
袋中装有编号为1,2,3的三个质地均匀、大小相同的球,从中随机取出一球记下编号后,放入袋中搅匀,再从袋中随机取出一球,两次所取球的的编号相同的概率为( )
A.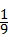 |
B.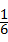 |
C.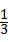 |
D.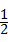 |
如图,点F是▱ABCD的边CD上一点,直线BF交AD的延长线与点E,则下列结论错误的是( )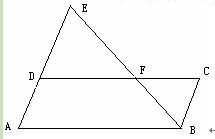
A.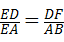 |
B.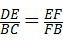 |
C. |
D.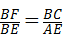 |
一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是( )
| A.5π | B.4π |
| C.3π | D.2π |