（本小题满分15分）如图1，抛物线
经过点A和点B.已知点A的坐标是（2，4），点B的横坐标是－2.
（1）求
的值及点B的坐标；
（2）设点D为线段AB上的一个动点，过D作x轴的垂线,垂足为点H.在DH的右侧作等边△DHG. 将过抛物线顶点Ｍ的直线记为
，设与x轴交于点N.
① 如图1，当动点D的坐标为(1，2)时，若直线
过△DHG的顶点G.求此时点N的横坐标是多少？
② 若直线与△DHG的边DG相交，试求点N横坐标的取值范围.
（本题10分）在平行四边形ABCD中，点E、F分别在AB、CD上，且AE=CF．
（1）求证：△ADE≌△CBF；
（2）若DF=BF，试判定四边形DEBF是何种特殊四边形？并说明理由．
（本题8分）已知，实数
，
，
在数轴上的位置如图所示，化简：
．
（本题10分）2014年我区正在推进的旅游产业中，对外宣传的优秀景点有：A：溱湖湿地公园；B：姜堰生态园；C：溱潼老街；D：北大街古文化区；E：“全球500佳”河横．区旅游管理部门对某月进入景点的人数情况调查统计，制成了两幅不完整的统计图（如图）．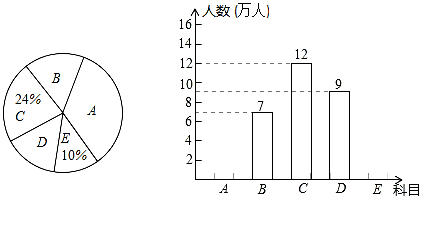
（1）求出这个月进入我区上述五个景点的总人数；
（2）请你补全频数分布直方图；
（3）求出扇统计图中A，溱湖湿地公园所对应的扇的圆心角的度数．
（本题10分）
（1）解分式方程：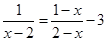
；
（2）先化简，再求值：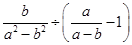
，其中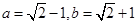
．
（本题10分）解下列一元二次方程：
（1）
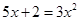（用公式法解）；（2）
．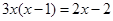