(12分) 在直角坐标系 中,点
中,点 到点
到点 ,
,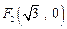 的距离之和是
的距离之和是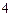 ,点
,点 的轨迹是
的轨迹是 ,直线
,直线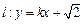 与轨迹
与轨迹 交于不同的两点
交于不同的两点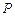 和
和 .⑴求轨迹
.⑴求轨迹 的方程;⑵是否存在常数
的方程;⑵是否存在常数 ,
,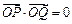 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2m的进出口,如图所示已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元)
⑴将y表示为x的函数;
⑵写出f(x)的单调区间,并证明;
⑶根据⑵,试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
已知ABCD四点的坐标分别为 A(1,0), B(4,3),
C(2,4),D(0,2)
⑴证明四边形ABCD是梯形;
⑵求COS∠DAB。
⑶设实数t满足( -t
-t )·
)· =0,求t的值。
=0,求t的值。
⑴已知cos(x+ )=
)= ,求cos(
,求cos( -x)+ cos2(
-x)+ cos2( -x)的值。
-x)的值。
⑵已知tanα=2,求
已知函数f(x)=-3sin2x-4cosx+2
⑴求f( )的值;
)的值;
⑵求f(x)的最大值和最小值。
集合A={ >1},B={
>1},B={ >2},A
>2},A B,求a的取值范围。
B,求a的取值范围。