某政府机关有在编人员100人,其中副处级以上干部10人,一般干部70人,工人20人,上级机关为了了解政府机构改革意见,要从中抽取一个容量为20的样本,试确定用何种方法抽取,如何抽取?
为了检验某种作业本的印刷质量,决定从一捆(40本)中抽取10本进行检查,利用随机数表抽取这个样本时,应按怎样的步骤进行?
某电台在因特网上就观众对某一节目的喜爱程度进行调查,参加调查的总人数为12 000人,其中持各种态度的人数如下表:
| 很喜爱 |
喜爱 |
一般 |
不喜爱 |
| 2 435 |
4 567 |
3 926 |
1 072 |
电视台为进一步了解观众的具体想法和意见,打算从中抽取60人进行更为详细的调查,应当怎样进行抽样?
在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交 作品的件数按5天一组分组统计,绘制了频率分布直方图(如图所示),已知从左到右各长方形高的比为2∶3∶4∶6∶4∶1,第三组的频数为12,请解答下列问题: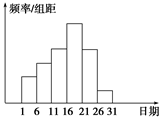
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率高?
某单位在岗职工共624人,为了调查工人用于上班途中的时间,该单位工会决定抽取10%的工人进行调查,请问如何采用系统抽样法完成这一抽样?