如图所示，BCDG是光滑绝缘的圆形轨道，位于竖直平面内，轨道半径为R，下端与水平绝缘轨道在B点平滑连接，整个轨道处在水平向左的匀强电场中，现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上，滑块受到的电场力大小为mg（g为重力加速度），滑块与水平轨道间的动摩擦因数为0.5，求：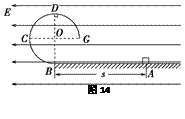
若滑块从水平轨道上距离B点s＝3R的A点由静止释放，滑块到达与圆心O等高的C点时速度为多大？
在(1)的情况下，求滑块到达C点时受到轨道的作用力大小；
改变s的大小，使滑块能沿圆周轨道滑行至与圆心等高的G点，求s应满足的条件。
水平桌面上质量为1 kg的物体受到2 N的水平拉力，产生1.5 m/s2的加速度。若水平拉力增至4 N，则物体将获得多大的加速度？
如图所示，传递带与水平面夹角θ=37°，并以v0=10m/s的速度运行着，在传送带的A端轻轻地放一小物体。若已知该物体与传送带
之间的滑动摩擦因数为μ=0.5，传送带A端到B端的距离S=16m，则小物体从A端运动到B端所需的时间可能是多少？（g=10m/s2）
三根不可伸长的相同的轻绳，一端系在半径为r0的环1上，彼此间距相等，绳穿过半径为r0的第2个圆环，另一端同样地系在半径为2r0的环3上，如图所示，环1固定在水平面上，整个系统处于平衡状态.试求第2个环中心与第3个环中心之间的距
离.(三个环都是用相同
的金属丝制作的，摩擦不计)
如一质量m=20kg的钢件，架在两根完全相同的、平行的长直圆柱上，如图5所示，钢件的重心与两柱等距，两柱的轴线在同一水平面内，圆柱的半径r=0.025m，钢件与圆柱间的滑动摩擦系数μ=0.20，两圆柱各绕自己的轴线做转向相反的转动，角速度ω=40rad/s，若沿平行于柱轴方向施加力推着钢件做速度为v0=0.05m/s的匀速运动，推力是多大？设钢件左右受光滑槽限制（图中未画出），不发生横向运动．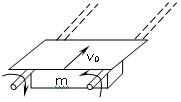
如图所示，一道峡谷宽为s＝400m，有一条长为L＝500m的钢索将两岸连接，一位质量为M＝60kg的越野运动员，在利用钢索、滑轮通过峡谷时，不慎在中途停下，如果不计钢索、滑轮的质量和运动员与钢索间的摩擦，求运动员停下时，钢索受到的拉力F是多大？（g取10m/s2）