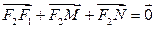(本小题满分14分)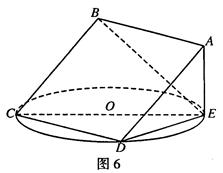
如图6,正方形ABCD所在平面与圆O所在平面
相交于CD,线段CD为圆O的弦,AE垂直于圆
O所在平面,垂足E是圆O上异于C、D的点,
AE=3,圆O的直径为9.
(1)求证:平面 ABCD ⊥平面 ADE;
(2)求二面角D—BC—E的平面角的正切值.
(本小题满分12分)
某公司为庆祝元旦举办了一次抽奖活动,现场准备的抽奖箱里放置了分别标有数字1000、800、600、0的四个球(球的大小相同).参与者随机从抽奖箱里摸取一球(取后即放回),公司即赠送与此球上所标数字等额的奖金(元),并规定摸到标有数字0的球时可以再摸一次,但是所得奖金减半(若再摸到标有数字0的球就没有第三次摸球机会),求一个参与抽奖活动的人可得奖金的期望值是多少元.
(本小题满分12分)
某公司近年来科研费用支出 万元与公司所获得利润
万元与公司所获得利润 万元之间有如下的统计数据:
万元之间有如下的统计数据:
 |
2 |
3 |
4 |
5 |
 |
18 |
27 |
32 |
35 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(3)试根据(2)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润.
参考公式:
(本小题满分14分)
已知函数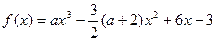
(1)当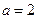 时,求函数
时,求函数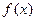 的单调性
的单调性
(2)当 时,试讨论曲线
时,试讨论曲线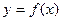 与
与 轴的公共点的个数。
轴的公共点的个数。
(本小题满分14分)
设椭圆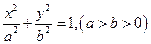 的左右焦点分别为
的左右焦点分别为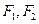 ,离心率
,离心率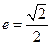 ,点
,点 在直线
在直线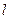 :
: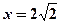 的左侧,且F2到l的距离为
的左侧,且F2到l的距离为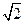 。
。
(1)求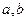 的值;
的值;
(2)设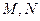 是
是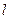 上的两个动点,
上的两个动点,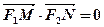 ,证明:当
,证明:当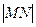 取最小值时,
取最小值时,