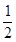某市热带植物园的门票价格规定如下表所列.
某校七年级(1)、(2)两个班学生共103人去该园参观, 其中七（1）班人数不少于30人且不多于50人. 经预算，若两班都以班为单位分别购票，则总共付
1950元.
| 购票人数 |
1～50人 |
51～100人 |
100人以上 |
| 每人门票价 |
20元 |
18元 |
15元 |
（1）若两班学生合在一起作为一个团体购票，则最多可以节省门票多少元？
（2）求两班各有多少名学生？
先观察图形，阅读相关文字后，再回答问题.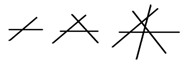
两条直线相交，最多有1个交点；
三条直线相交，最多有3个交点；
四条直线相交，最多有6个交点；
…… ……
问题：10条直线相交，最多有几个交点？
小张、小王、小李同时从湖边同一地点出发，绕湖行走．小张的速度是5.4千米/小时，小王的速度是4.2千米/小时，他们两人同向行走，小李与他们反向行走，半小时后小李和小张相遇，再经过5分钟，小李与小王相遇．那么绕湖一周的行程是多少千米？
甲、乙两品牌服装的单价分别为a元和b元，现实行打折销售，甲种服装按8折（即原价的80%）销售，乙种服装按7折销售，若购买两种品牌服装各一件，共需多少元？
已知甲数是乙数的相反数的2倍，设乙数为x, 用关于x的代数式表示甲数.
用代数式表示：
⑴x的2倍与y的3倍的差
⑵x的