在一个不透明的盒子里装有除颜色外完全相同的黑、白两种球共40个，小明做摸球实验，他将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据:
| 摸球的次数 |
100 |
200 |
300 |
500 |
800 |
1000 |
3000 |
| 摸到白球的频数 |
65 |
|
178 |
302 |
481 |
599 |
1803 |
| 摸到白球的频率 |
0.65 |
0.62 |
0.593 |
0.604 |
0.601 |
0.599 |
|
（1）将数据表补充完整；
（2）请你估计: 随着实验次数
的增加，摸到白球的频率特点是 ,这个频率将会接近 （精确到0.1）；
（3）假如你摸一次，你摸到白球的机会是 ；
（4）试估算盒子里黑、白两种颜色的球各有多少个？
选择适当的方法分解下列多项式
（1）x2+9y2+4z2﹣6xy+4xz﹣12yz
（2）（a2+5a+4）（a25a+6）﹣120．
当m取何值时，函数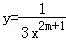
是反比例函数？
已知函数y=（m﹣1）x|m|﹣2是反比例函数．
（1）求m的值；
（2）求当x=3时，y的值．
已知变量y与变量x之间的对应值如下表：
x … 1 2 3 4 5 6 …
y … 6 3 2 1.5 1.2 1 …
试求出变量y与x之间的函数关系式： ．
在生活中不难发现这样的例子：三个量a，b和c之间存在着数量关系a=bc．例如：长方形面积=长×宽，匀速运动的路程=速度×时间．
（1）如果三个量a，b和c之间有着数量关系a=bc，那么：
①当a=0时，必须且只须 ；
②当b（或c）为非零定值时，a与c（或b）之间成 函数关系；
③当a（a≠0）为定值时，b与c之间成 函数关系．
（2）请你编一道有实际意义的应用性问题，解题所列的方程符合数量关系：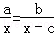
，（其中x为未知数，a，b，c为已知数，不必解方程）．