在三角形ABC中,根据下列条件解三角形,其中有一个解的是()
| A.b=7,c=3,C=300 | B.b=5,c= 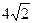 ,B=450 ,B=450 |
C.a=6,b=  ,B=600 ,B=600 |
D.a=20,b=30,A=300 |
在等差数列{an}中,a1 =8,a5 =2,若在每相邻两项间各插入一个数,使之成等差数列,那么新的等差数列的公差()
A.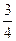 B
B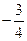 C
C 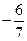 D -1
D -1
已知a,b,c成等比数列, a,x,b成等差数列, b,y,c也成等差数列,
则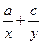 的值为()
的值为()
| A.1 | B.2 | C.3 | D.4 |
已知函数f(x)=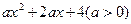 ,若
,若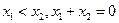 ,则()
,则()
A.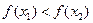 |
B.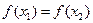 |
C.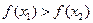 |
D.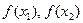 的大小不能确定 的大小不能确定 |
P(x,y)是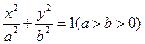 上任意一点,
上任意一点,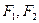 是其两个焦点,则
是其两个焦点,则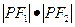 的取值范围是()
的取值范围是()
A. |
B.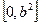 |
C.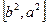 |
D.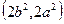 |