已知：如图9，在△ABC中，AB＝AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E。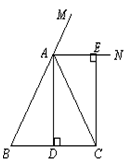
（1）求证：四边形ADCE为矩形；
（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明。
解方程：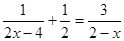
计算：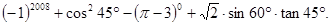
A、B两地果园分别有苹果10吨和40吨，全部运送到C、D两地，而C、D两地分别需要苹果15吨和35吨；已知从A、B地到C、D地的运价如下表：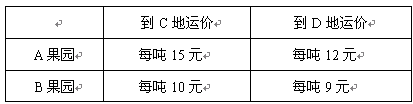
（1）若从B果园运到C地的苹果为x吨，则从B果园运到D地的苹果为________吨；从A果园将苹果运往D地的运输费用为__________________________元.
（2）用含x的式子来表示出总运输费（要求：列出算式，并化简）
将连续的偶数2，4，6，8，10，…，排成如下的数表．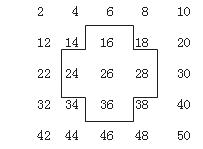
(1)十字框中的五个数的和与中间的数 26 有什么关系?
(2)设中间的数为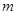
，用代数式表示十字框中的五个数之和；
（3）十字框中的五个数之和能等于 2060 吗？若能，请写出这五个数；若不能，请说明理由．
AB边上的高CD；